GI VR/AR 2006
Passive-Active Geometric Calibration for View-Dependent Projections onto Arbitrary Surfaces
First presented at the Third Workshop Virtual
and Augmented Reality of the GI-Experts Group
AR/VR 2006,
extended and revised for JVRB
urn:nbn:de:0009-6-11762
Abstract
In this paper we present a hybrid technique for correcting distortions that appear when projecting images onto geometrically complex, colored and textured surfaces. It analyzes the optical flow that results from perspective distortions during motions of the observer and tries to use this information for computing the correct image warping. If this fails due to an unreliable optical flow, an accurate -but slower and visible- structured light projection is automatically triggered. Together with an appropriate radiometric compensation, view-dependent content can be projected onto arbitrary everyday surfaces. An implementation mainly on the GPU ensures fast frame rates.
Keywords: dynamic geometric calibration, projector-camera systems, optical flow
Subjects: Camera, Projector
Projecting images onto surfaces that are not optimized for projections becomes more and more popular. Such approaches will enable the presentation of graphical, image or video content on arbitrary surfaces. Virtual reality visualizations may become possible in everyday environments - without specialized screen material or static screen configurations (cf. figure 1 ). Upcoming pocket projectors will enable truly mobile presentations on all available surfaces of furniture or papered walls. The playback of multimedia content will be supported on natural stonewalls of historic sites without destroying their ambience through the installations of artificial projection screens.
Several real-time image correction techniques have been developed that carry out geometric warping [ BWEN05 ], radiometric compensation [ BEK05, NPGB03 ], and multi-focal projection [ BE06 ] for displaying images on complex surfaces without distortions.
As long as the geometry of a non-trivial (e.g. multi-planar), non-textured surface is precisely known, the geometric warping of an image can be computed. Projecting the pre-warped image from a known position ensures the perception of an undistorted image from a known perspective (e.g., of a head-tracked observer or a calibrated camera). Hardware accelerated projective-texture mapping is a popular technique that has been applied for this purpose several times[ RBY99 ]. As soon as the surface geometry becomes geometrically more complex or the surface is textured, projective texture-mapping will fail due to imprecisions in the calculations. Minimization errors lead to small misregistrations between projector-pixels and corresponding surface pigments. In addition, projective texture-mapping models a simple pinhole geometry and does not consider the lens distortion of the projector optics. All of this leads to calibration errors in the order of several pixels, and finally to well visible blending artifacts of compensated pixels that are projected onto wrong surface pigments.
Several techniques have been introduced that ensure a precise pixel-individual warping of the image by measuring the mapping of each projector pixel to the corresponding pixels of a calibration camera when being projected onto a complex surface [ BEK05, PA82 ]. Structured light projection techniques are normally being used for determining these correspondences. This leads to pixel-precise look-up operations instead of imprecise image warping computations. The surface geometry does not have to be known. However, since the look-up tables are only determined for one perspective (i.e., the perspective of the calibration camera), view-dependent applications are usually not supported. But this becomes essential for supporting moving observers.
In this paper we describe an online image-based approach for view-dependent warping of images being projected onto geometrically and radiometrically complex surfaces. It continuously measures the image distortion that arises from the movement of an observer by computing the optical flow between the distorted image and an estimated optimal target image. If the distortion is low, the optical flow alone is used for image correction. If the distortion becomes too high, a fast structure light projection is automatically triggered for recalibration.
Camera-based geometric calibration techniques can be categorized into online or offline methods. While an offline calibration determines the calibration parameters (such as the projector-camera correspondence) in a separate step before runtime, an online calibration performs this task continuously during runtime. A lot of previous work has been done on offline calibration - but little on online techniques.
Active offline calibration techniques usually rely on structured light projection to support enhanced feature detection [ PA82, CKS98 ]. For simple surfaces with known geometry the geometric image warping can be computed with beforehand determined constant calibration parameters. Examples are homography matrices (for planar surfaces [ YGH01, CSWL02 ]) or intrinsic and extrinsic projector parameters for non-trivial, non-complex surfaces with known geometry [ RBY99 ]. These techniques also support a moving observer since the image warping is adapted to the users position in real-time. For geometrically complex and textured surfaces with unknown geometry, projector-camera correspondences can be measured offline for a discrete number of camera perspectives. During runtime, the correct image warping is approximated in real-time by interpolating the measured samples depending on the observer′s true perspective [ BWEN05 ].
Online techniques can apply imperceptible structured light patterns that are seamlessly embedded into the projected image [ CNGF04, RWC98 ]. This can be achieved by synchronizing a camera to a well-selected time-slot during the modulation sequence of a DLP projector [ CNGF04 ]. Within this time-slot the calibration pattern is displayed and detected by the camera. Since such an approach requires modifying the original colors of the projected image, a loss in contrast can be an undesired side effect. Other techniques rely on a fast projection of images that cannot be perceived by the observer. This makes it possible to embed calibration patterns in one frame and compensate them with the following frame. Capturing altering projections of colored structured light patterns and their complements allows the simultaneous acquisition of the scene′s depth and texture without loss of image quality [ WWC05 ].
A passive online method was described for supporting a continuous autocalibration on a non-trivial display surface [ YW01 ]. Instead of benefiting from structured light projection, it directly evaluates the deformation of the image content when projected onto the surface. This approach assumes a calibrated camera-projector system and an initial rough estimate of the projection surface to refine the reconstructed surface geometry iteratively.
This section describes our online calibration approach. It represents a hybrid technique, which combines active and passive calibration.
For initializing the system offline a calibration camera must be placed at an arbitrary position - capturing the screen surface. The display area on the surface can then be defined by outlining the two-dimensional projection of a virtual canvas, as it would be seen from the calibration camera′s perspective. The online warping approach ensures that -from a novel perspective- the corrected images appear as to be displayed on this virtual canvas (off-axis). It also tries to minimize geometric errors that result from the underlying physical (non-planar) surface. Theoretically it is also possible to create a frontal view in such a way that the image appears as a centered rectangular image plane (on-axis). However, clipping with the physical screen area may occur in this case.
For the initial calibration camera the pixel correspondence between camera pixels and projector pixels is determined by projecting a fast point pattern. This results in a two-dimensional look-up table that maps every projector-pixel to its corresponding camera-pixel. This look-up table can be stored in a texture and passed to a fragment shader for performing a pixel displacement mapping [ BEK05 ]. The warped image is projected onto the surface and appears undistorted from the perspective of the calibration camera.
In addition the surface reflectance and the environment light contribution are captured from the calibration camera position. These parameters are also stored in texture maps, which are passed to a fragment shader that carries out a per-pixel radiometric compensation to avoid color blending artifacts when projecting onto a textured surface [ BEK05 ].
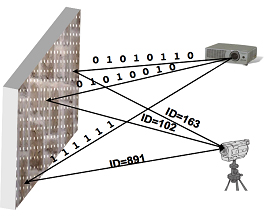
For determining the correspondences between projector and camera pixels, a fast point pattern technique is used (cf. figure 2 ).
A grid of n points is projected simultaneously. Thereby, each point can be turned on or off - representing a binary 1 or 0 (cf. figure 3 -left). Projecting a sequence of point images allows transmitting a binary code at each grid position optically from projector to camera. Each code represents a unique identifier that establishes the correspondence between points on both image planes - the one of the projector and the one of the camera. Depending on the resolution of the grid the code words differ in length. Thus, a minimum of ld(n) images have to be projected to differentiate between the n grid points. Additional bits can be added for error-detection.
To create a continuous lookup table for each projector pixel from the measured mappings of the discrete grid points, tri-linear interpolation is being applied. To benefit from hardware acceleration of programmable graphic cards this lookup table is rendered with a fragment shader into a 16bit texture. The resulting displacement map stores the required x,y-displacement of each projector pixel in the r,g channels of the texture. To achieve a further speed-up, spatial coding can be used instead of a simple binary pattern. Projecting two distinguishable patterns per point (e.g., a circle and a ring) allows encoding three states per position and image (cf. figure 3 -right). For this case, the minimal number of projected images required to encode n points drops to ld(n)/2.
We found that more sophisticated coding schemes (e.g., using color, intensities or more complicated spatial patterns) are difficult to differentiate reliably when projecting onto arbitrarily colored surfaces. This is in particular the case if off-the-shelf hardware is being applied. With a conventional and unsynchronized camcorder (175ms latency) we can scan 900 grid points in approximately one second (by sending two bits of the codeword per projected pattern).
Once the system is calibrated we can display geometrically corrected and radiometrically compensated images as long as projector and camera/observer are stationary [ BEK05 ]. As soon as the observer moves away from the sweet spot of the calibration camera, geometric distortions become perceivable. Note that as long as the surface is diffuse, radiometric distortions do not arise from different positions.
For the following we assume that the camera is attached to the observer′s head - matching his/her perspective. This can be realized by mounting a lightweight pen camera to the worn stereo goggles (in case active stereo projection is supported [ BWEN05 ]). Consequently, the resulting distortion can be continuously captured and evaluated. As described in section 3.1 , a pixel correspondence between the initial calibration camera C0 and projector P exists. For a new camera position (Ci ) that results from movement, another pixel correspondence between Ci and C0 can be approximated based on optical flow analysis. A mapping from Ci to P is then given over C0 . Thus, two look-up tables are used: one that stores camera-to-camera correspondences Ci → C0 , and one that holds the camera-to-projector correspondences C0 → P.
Our algorithm can be summarized as follows and will be explained in more detail below:
1: if camera movement occurs
2: if camera movement stops
3: calculate optical flow between initial
camera image and current camera image
4: filter optical flow vectors
5: calculate homography from optical flow
6: transform default image with homography
7: calculate optical flow between current
camera image and transformed image
8: calculate displacement from optical flow
9: endif
10: endif
For computing Ci → C0 the system tries to find feature correspondences between the two camera perspectives (Ci and C0 ) and computes optical flow vectors. This step is triggered only when the observer stops moving in a new position (line 2), which is characterized by constant consecutive camera frames.
Since the image captured from Ci is geometrically and perspectively distorted over the surface (cf. figure 4 b), the correct correspondences Ci → C0 cannot be determined reliably from this image. Therefore, a corrected image for the new perspective Ci has to be computed first. Since neither the camera nor the observer is tracked this image can only be estimated. The goal is to approximate the perspective projection of the virtual canvas showing the geometrically undistorted content from the perspective of Ci (cf. figure 4 d). Thereby, the virtual canvas has to appear as to be static in front or behind the surface. Two steps are carried out for computing the perspectively corrected image (line 3-6) - an image plane transformation followed by a homography transformation:
First, the original image content is texture mapped onto a quad that is transformed on the image plane of C0 in such a way that it appears like an image projected onto a planar surface seen from the initial camera position (line 3). Note, that this first transformation does not contain the perspective distortion. It is being carried out initially to increase the quality of feature tracking algorithms during the following optical flow analysis. Consequently, the optical flow of a discrete number of detectable feature points between the transformed texture and the image captured from Ci can be computed on the same image plane. Unreliable optical flow vectors are filtered out (line 4) by comparing their lengths and directions. Furthermore, the relation of the feature positions in both images will be considered. Vectors marked as unreliable are deleted. The remaining ones allow us to compute displacements for a discrete set of feature points between the distorted image from Ci and the undistorted image from C0 .
Figure 4. Passive calibration steps: correct image (a), geometric distortion for new camera position (b), computed optical flow vectors (c), geometrically corrected image based on optical flow analysis (d).
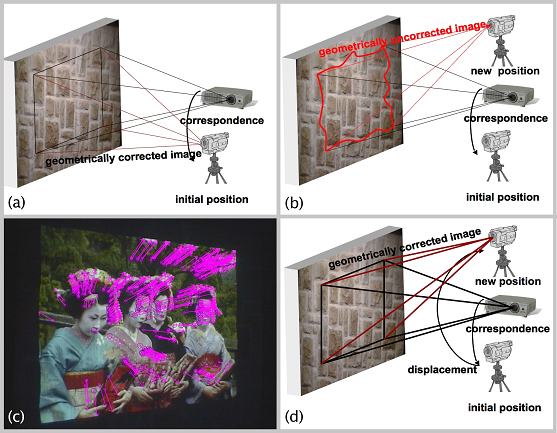
The second step uses these two-dimensional correspondences for computing a homography matrix that transforms the geometrically undistorted image from the perspective of C0 into the perspective of Ci to approximate the missing perspective distortion. Since the homography matrix describes a transformation between two viewing positions (C0 → Ci ) over a plane, this transformation is only an approximation, which is sufficient to estimate the ideal image at the new camera position. To avoid an accumulation of errors the homography matrix that approximates the mapping between C0 and the new camera position Ci is applied.
A second optical flow analysis between the image captured from Ci and the perspectively corrected image computed via the homography matrix for Ci is performed next (line 7). While the first image contains geometric distortions due to the non-planar screen geometry, the latter one does not. Both images, however, approximate the same perspective distortion. Unreliable flow vectors are filtered out again. The determined optical flow vectors allows -once again- determining the displacements for a number of discrete feature pixels between both images. We apply a pyramidal implementation of the Lucas Kanade Feature Tracker [ Bou99 ] for optical flow analysis. It enables to quickly determine large pixel flows with sub pixel accuracy. We decided to use the pyramid-based Lucas-Kanade feature tracker algorithm. Other algorithms that we tested required more time for calculation, or were not able to calculate the optical flow for large displacements. Since the selected algorithm calculates the optical flow only for a sparse feature set, Delaunay triangulation and bilinear interpolation of the resulting flow positions have to be applied to fill empty pixel positions. This makes it finally possible to establish the correspondences between each visible image pixel in Ci and C0 . Since the mapping between C0 and P is known, the mapping from Ci to P is implied. Only the optical flow calculations are carried out on the CPU. Both look-up tables are stored in texture maps and processed by a fragment shader that performs the actual pixel displacement mapping on the GPU in about 62ms.
Animations, movies or interactive renderings are paused during these steps to ensure equal image content for all computations. Thus, new images are continuously computed for perspective C0 (i.e., rendered into the virtual canvas defined from C0 ), warped into perspective Ci and finally transformed to the perspective of the projector P. For implementation reasons, the shader lookup operations are applied in a different order: P → C0 → Ci
If the passive calibration method becomes too imprecise the accurate active calibration is triggered automatically to reset the mapping C0 → P. The quality of the passive correction can be determined by evaluating the amount of features with large eigenvalues and the number of valid flow vectors. If both drop under a pre-defined threshold the offline calibration will be triggered. The same active calibration technique as described in section 3.2 can be applied. The perspective change that is due to the camera movement, however, has to be considered.
As for the passive method, we try to simulate the perspective distortion between the previous C0 and Ci by computing a homography matrix. The original image can then be warped from C0 to Ci by multiplying every pixel in C0 with this matrix. To determine the homography matrix we have to solve a linear equation system via least squares method for a minimum of nine sample points with known image coordinates in both perspectives. Since the camera-projector point correspondences in both cases are known (the original C0 → P from the initial active calibration, and Ci → P from a second active calibration that is triggered if the passive calibration fails), the mapping from C0 to Ci is implicitly given for every calibration point. As mentioned in section 3.3 the mapping from C0 to Ci by using the homography matrix is only an approximation.
In addition to the geometric image distortion, the projected pixels′ colors are blended by the reflectance of underlying surface pigments. This results in color artifacts if the surface has a non-uniform color and a texture. To overcome these artifacts, the pixels′ colors are modified in such a way that their corresponding blended reflection on the surfaces approximates the original color. If the surface is Lambertion, this is view-independent, and a variety of radiometric compensation techniques can be applied [ BEK05, NPGB03, FGN05 ]. To compensate small view-dependent effects (such as light specular highlights), image-based techniques offer appropriate approximations [ BWEN05 ].
All of these techniques initially measure parameters, such as the environment light and projector contributions as well as the surface reflectance via structured light and camera feedback. We carry out our radiometric compensation computations for multiple projectors [ BEK05 ] on a per-pixel basis directly the GPU - within the same fragment shader that performs the per-pixel displacement mapping (see section 3.3 ). Since we assume diffuse surfaces we can measure the required parameters during the initial calibration step (see sections 3.1 and 3.2 ) and map them (i.e., via C0P) to the image plane of the projector - which is static. Therefore, these parameters are constant all the time and a recalibration after camera movement is not necessary.
Note that all images that are captured for computing optical flow vectors (section 3.3 ) are radiometrically compensated to avoid color artifacts that would otherwise lead to an incorrect optical flow.
We tested our method on a natural stone wall screen with a complex geometry and a textured surface (cf. figure 5 d). The projection resolution was XGA.
Figure 5. Passive calibration results: ideal image (a) and close-up (e), uncorrected image (b) and close-up (f), corrected image (c) and close-up (g), image without radiometric compensation under environment light (d), visualized error maps for uncorrected (h) and corrected (i) case.

The system was initially calibrated for C0 by using the fast structured light method for estimating the projector-camera-correspondence (which maps C0 → P) and by measuring the parameters necessary for the radiometric compensation. In total this process took about 2 seconds when applying an unsynchronized camera with a camera delay of 175ms. If a camera movement is detected the passive calibration is triggered. The duration for calculating the optical flow depends on the number of features, and was about 60ms for 800 features in our case (on a P4 2,8GHz).
An example of the result that is based on optical flow analysis is visualized in figure 5. While figure 5 a illustrates the ideal result as would appear on a plane surfaces, figure 5 b shows he uncorrected result as being projected into the stone wall (note that radiometric compensation is carried out in both cases). Figure 5 c presents the result after the passive calibrations. A reduction of the geometric error compared to figure 5 b is clearly visible. The remaining error between corrected (figure 5 c) and ideal (figure 5a) image can be determined by computing the per-pixel difference between both images. While figure 5 h represents the difference between uncorrected and ideal image, figure 5 i shows the difference between correct and ideal image.
In this paper we have presented a hybrid calibration technique for correcting view-dependent distortions that appear when projecting images onto geometrically and radiometrically complex surfaces. During camera movement (i.e., movement of the observer′s target perspective), the optical flow of the displayed image is analyzed. If possible, a per-pixel warping of the image geometry is carried out on the fly - without projecting visible light patterns. However, if the optical flow is too unreliable, a fast active calibration is triggered automatically. Together with an appropriate radiometric compensation, this allows perceiving undistorted images, videos, or interactively rendered (monoscopic or stereoscopic) content onto complex surfaces from arbitrary perspectives. We believe that for domains such as virtual reality and augmented reality this holds the potential of avoiding special projection screens and inflexible screen configurations. Arbitrary everyday surfaces can be used instead - even complex ones.
Since all parameters for radiometric compensation are mapped to the perspective of the projector, they become independent to the observer′s perspective. Consequently, multi-projector techniques for radiometric compensation [ BEK05 ] and multi-focal projection [ BE06 ] are supported.
Our future work will focus on replacing the active calibration step that yet displays visible patterns by techniques that project imperceptible patterns [ CNGF04, RWC98 ]. This will lead to an invisible and continuous geometric and radiometric calibration process. The passive part of this process will ensure fast update rates - especially for small perspective changes. The active part sill provides an accurate solution at slower rates. Both steps might also be parallelized to allow selecting the best solution available at a time.
This project is supported by the Deutsche Forschungsgemeinschaft (DFG) under contract number PE 1183/1-1.
[BE06] Multi-Focal Projection: A Multi-Projector Technique for Increasing Focal Depth, IEEE Transactions on Visualization and Computer Graphics (2006), no. 4, 658—667, issn 1077-2626.
[BEK05] Embedded Entertainment with Smart Projectors, IEEE Computer (2005), no. 1, 48—55, issn 0018-9162.
[Bou99] Pyramidal Implementation of the Lucas Kanade Feature Tracker Description of the Algorithm, Intel Corporation, Microprocessor Research Labs, 1999.
[BWEN05] Enabling View-Dependent Stereoscopic Projection in Real Environments, Proc. of IEEE/ACM International Symposium on Mixed and Augmented Reality (ISMAR'05), 2005, pp. 14—23, isbn 0-7695-2459-1.
[CKS98] Range imaging with adaptive color structured light, IEEE Transactions on Pattern analysis and machine intelligence (1998), no. 5, 470—480, issn 0162-8828.
[CNGF04] Embedding Imperceptible Patterns into Projected Images for Simultaneous Acquisition and Display, IEEE and ACM International Symposium on Mixed and Augmented Reality (ISMAR04), 2004, Arlington, pp. 100—109, isbn 0-7695-2191-6.
[CSWL02] Scalable alignment of large-format multi-projector displays using camera homography trees, Proceedings of IEEE Visualization (IEEE VIS'02), 2002, pp. 339—346, issn 1070-2385.
[FGN05] A Projector-Camera System with Real-Time Photometric Adaptation for Dynamic Environments, Proc. of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05), 2005, , pp. 814—821 issn 1063-6919.
[NPGB03] A Projection System with Radiometric Compensation for Screen Imperfections, Proc. of International Workshop on Projector-Camera Systems, 2003.
[PA82] Surface measurement by space-encoded projected beam systems, Computer Graphics and Image Processing (1982), no. 1, 1—17, issn 0146-664X.
[RBY99] Multi-projector displays using camera-based registration, Proc. of IEEE Visualization (IEEE Vis'99), 1999, pp. 161—168, isbn 0-7803-5897-X.
[RWC98] The office of the future: a unified approach to image-based modeling and spatially immersive displays, Proc. of of the 25th annual conference on Computer graphics and interactive techniques (SIGGRAPH '98), 1998, pp. 179—188, isbn 0-89791-999-8.
[WWC05] Scalable 3D Video of Dynamic Scenes, The Visual Computer (2005), no. 8-10, 629—638, issn 1432-2315.
[YGH01] PixelFlex: A Reconfigurable Multi-Projector Display System, IEEE Visualization, 2001, pp. 167—174, isbn 0-7803-7200-X.
[YW01] Automatic and Continuous Projector Display Surface Calibration Using Every-Day Imagery, Proceedings of 9th International Conf. in Central Europe in Computer Graphics, Visualization, and Computer Vision WSCG 2001, Plzen, 2001, isbn 80-7082-711-4.
Volltext ¶
-
 Volltext als PDF
(
Größe:
861.1 kB
)
Volltext als PDF
(
Größe:
861.1 kB
)
Lizenz ¶
Jedermann darf dieses Werk unter den Bedingungen der Digital Peer Publishing Lizenz elektronisch übermitteln und zum Download bereitstellen. Der Lizenztext ist im Internet unter der Adresse http://www.dipp.nrw.de/lizenzen/dppl/dppl/DPPL_v2_de_06-2004.html abrufbar.
Empfohlene Zitierweise ¶
Stefanie Zollmann, Tobias Langlotz, and Oliver Bimber, Passive-Active Geometric Calibration for View-Dependent Projections onto Arbitrary Surfaces. JVRB - Journal of Virtual Reality and Broadcasting, 4(2007), no. 6. (urn:nbn:de:0009-6-11762)
Bitte geben Sie beim Zitieren dieses Artikels die exakte URL und das Datum Ihres letzten Besuchs bei dieser Online-Adresse an.