No section
Real-time depth camera tracking with CAD models and ICP
urn:nbn:de:0009-6-44132
Abstract
In recent years, depth cameras have been widely utilized in camera tracking for augmented and mixed reality. Many of the studies focus on the methods that generate the reference model simultaneously with the tracking and allow operation in unprepared environments. However, methods that rely on predefined CAD models have their advantages. In such methods, the measurement errors are not accumulated to the model, they are tolerant to inaccurate initialization, and the tracking is always performed directly in reference model's coordinate system. In this paper, we present a method for tracking a depth camera with existing CAD models and the Iterative Closest Point (ICP) algorithm. In our approach, we render the CAD model using the latest pose estimate and construct a point cloud from the corresponding depth map. We construct another point cloud from currently captureddepth frame, and find the incremental change in the camera pose by aligning the point clouds. We utilize a GPGPU-based implementation of the ICP which efficiently uses all the depth data in the process. The method runs in real-time, it is robust for outliers, and it does not require any preprocessing of the CAD models. We evaluated the approach using the Kinect depth sensor, and compared the results to a 2D edge-based method, to a depth-based SLAM method, and to the ground truth. The results show that the approach is more stable compared to the edge-based method and it suffers less from drift compared to the depth-based SLAM.
Keywords: Augmented reality, Mixed reality, Tracking, Pose estimation, Depth camera, KINECT, CAD model, ICP
Keywords: CAD model, ICP, KINECT, Mixed Reality, Tracking, Pose Estimation, Depth Camera
SWD: Kinect, Mixed Reality,
Augmented reality (AR) provides an intuitive way to show relevant information to guide a user in complex tasks like maintenance, inspection, construction and navigation [ Azu97, vKP10 ]. In AR, the image streams are superimposed in real-time with virtual information that is correctly aligned with the captured scene in 3D. For example, assembly instructions can be virtually attached to an object of interest in the real world, or an object of the real world can be highlighted in the augmented camera image [ HF11 ]. In augmented assembly, it is also important to visualize the quality of the work: the user may have forgotten to install a part, the part may have been installed in a wrong position, or a wrong part may have been used. For this purpose, the real scene and its digital counterpart have to be compared to find the possible 3D differences between them [ KBKF13 ]. Furthermore, diminished reality is a technique where the user's view is altered by removing real objects from the images and possibly replacing them with virtual content [ MF01 ]. For example, in AR assisted decoration, existing furniture is removed and replaced with digital furniture to aid in planning a new room lay-out.
AR, diminished reality and other related applications require that the position and the orientation (pose) of the camera (user's view) can be estimated and tracked precisely in real-time. The most common approach is to analyze the captured 2D images, and various optical tracking methods have been proposed from easily detectable fiducial markers to natural image features [ ZDB08, LF05 ]. Simultaneous localization and mapping (SLAM) approaches are attractive since they do not require any preparation of the environment in order to operate. Instead, the scene model is reconstructed from the image observations while simultaneously tracking the camera [ BBS07, KM07, DRMS07 ]. However, in most of the AR applications, the camera pose has to be defined exactly in the reference object's coordinate frame, and model-based tracking solutions are desirable. The model-based tracking methods aim to fit features (typically edges) extracted from the camera image to 2D projections of the 3D model of the reference target to estimate the 6-DoF transformation between them [ LF05 ].
A common requirement of 2D image-based camera pose estimation approaches is that the captured scene needs to provide features which are visible in the 2D camera image and which can be analyzed in order to estimate the camera pose. For example, due to a lack of detectable 2D features, it is very difficult to estimate the camera pose if the captured scene has untextured monochromatic surfaces or the lighting conditions are difficult. Strong shadows are indistinguishable from actual edges, reflections of light disturb the feature detection and dim illumination increases the noise level. In recent years, 2D imaging has been complemented by the development of depth cameras. They operate at up to 30 frames per second, and measure each pixel's distance from the camera to the object in the real world [ HLCH12, GRV13 ]. While initially very expensive and rather inaccurate, technological advancements have led to the development of cheap and more precise depth cameras for the consumer mass market. Depth sensors have become commodity hardware and their availability, price and size are nowadays close to conventional 2D cameras.
Depth cameras have clear advantages in terms of camera pose estimation and tracking. They are tolerant to common problems that appear in monocular camera tracking including changes in illumination, repetitive textures and lack of features. Typical depth camera technologies (time-of-flight, structured light) rely on active illumination so they can also operate in low light conditions. The appearance of the depth maps depend mainly on the 3D geometry of the scene, and thus, depth cameras are attractive devices for camera tracking. Recent research on depth camera based tracking focus mainly on SLAM and other approaches that create the reference model during the operation. Such trackers can perform in unprepared environments, but they still have drawbacks compared to the trackers that utilize predefined models.
In this paper, we present and evaluate a model-based tracking method for depth cameras that utilizes predefined CAD models to obtain the camera pose. We take the advantage of precise CAD models commonly available in industrial applications, and apply iterative closest point (ICP) algorithm for registering the latest camera pose with the incoming depth frame. We use direct method, where all the depth data is used without explicit feature extraction. With a GPGPU implementation of the ICP, the method is fast and runs in real time frame rates. The main benefits of the proposed approach are:
-
In contrast to monocular methods, the approach is robust with both textured and non-textured objects and with monochromatic surfaces. The approach does not require any explicit feature extraction from the (depth) cameras frames.
-
In contrast to depth-based SLAM methods, measurement and tracking errors are not accumulated, the method is faster, and it always tracks directly in the reference target's coordinate system. The approach is robust for differences between the CAD model and the real target geometry. Thus, it can be used in applications such as difference detection for quality inspection.
-
Virtually any 3D CAD model can be used for tracking. The only requirement is that the model needs to be rendered, and that the corresponding depth map has to be retrieved from the depth buffer for the tracking pipeline.
The remainder of this paper is structured as follows: in Section 2, we give an overview of model-based optical tracking methods as well as methods utilizing depth cameras. In Section 3, we detail our CAD model-based depth camera tracking approach. Section 4 provides an evaluation of the method. We describe the datasets and the evaluation criteria, and compare the results to the ground truth, to a 2D edge-based method, and to a depth-based SLAM method. In Section 5 we present the results, and experiment with the factors that affect to the performance of the approach. Finally, in Section 6, the results are discussed and a brief description of future work is presented.
Edges are relatively invariant to illumination changes, and they are easy to detect from the camera images. There are multiple studies that focus on model-based monocular tracking using edges. In the typical approach, the visible edges of the 3D CAD model are projected to the camera image using the camera pose from a previous time step, and aligned with the edges that are extracted from the latest camera frame. The change of the pose between the two consecutive frames is found by minimizing the reprojection error of the edges. One of the first real-time edge-based implementations was presented in [ Har93 ], where a set of control points are sampled from the model edges and projected to the image. The algorithm then searches for strong image gradients from the camera frame along the direction of control point normals. The maximum gradient is considered to be the correspondence for the current control point projection. Finally, the camera pose is updated by minimizing the sum of squared differences between the point correspondences.
The method presented in [ Har93 ] is sensitive to outliers (e.g. multiple strong edges along the search line, partial occlusions), and a wrong image gradient maximum may be assigned to a control point leading to a wrong pose estimate. Many papers propose improvements to the method. In [ DC02 ], robust M-estimators were used to lower the importance of outliers in the optimization loop, a RANSAC scheme was applied e.g. in [ AZ95, BPS05 ], and a multiple hypothesis assignment was used in conjunction with a robust estimator e.g. in [ WVS05 ]. In [ KM06 ], a particle filter was used to find the globally optimal pose. The system was implemented using a GPU which enabled fast rendering of visible edges as well as efficient likelihood evaluation of each particle. Edge-based methods have also been realized with point features. In [ VLF04 ], 3D points lying on the model surface were integrated with the pose estimation loop together with the edges.
The Kinect sensor was the first low-cost device to capture accurate depth maps at real-time frame rates. After it was released, many researcher used the sensor for real-time depth-based and RGB-D based SLAM. Many of the studies incorporate iterative closest point (ICP) in the inter-frame pose update. In ICP based pose update, the 3D point pairing is a time consuming task and several variants have been proposed to reduce the computational load for real-time performance. In KinectFusion [ NIH11 ], an efficient GPU implementation of the ICP algorithm was used for the pose update in depth-based SLAM. The ICP variant of the KinectFusion utilizes projective data association and point-to-plane error metrics. With a parallelized GPU implementation, all of the depth data can be used efficiently without explicitly selecting the point correspondences for the ICP. In [ TAC11 ], a bi-objective cost function combining the depth and photometric data was used in ICP for visual odometry. As in KinectFusion, the method uses an efficient direct approach where the cost is evaluated for every pixel without explicit feature selection. The SLAM approach presented in [ BSK13 ] represents the scene geometry with a signed distance function, and finds the change in camera pose parameters by minimizing the error directly between the distance function and observed depth leading to faster and more accurate result compared to KinectFusion.
SLAM and visual odometry typically utilize the entire depth images in tracking and the reference model is reconstructed from the complete scene. In object tracking however, the reference model is separated from the background and the goal is to track a moving target in a possibly cluttered environment, and with less (depth) information and geometrical constraints. In [ CC13 ], a particle filter is used for real-time RGB-D based object tracking. The approach uses both photometric and geometrical features in a parallelized GPU implementation, and uses point coordinates, normals and color for likelihood evaluation. ICP was used in [ PLW11 ] for inter-frame tracking of the objects that are reconstructed from the scene on-line. Furthermore, the result from ICP is refined by using the 3D edges of the objects similarly to [ DC02 ].
Although SLAM enables straightforward deployment of an augmented reality system, model-based methods still have their advantages compared to SLAM. Especially in industrial AR applications, it is important that the camera pose is determined exactly in the target object's coordinate system so that the virtual content can be rendered in exactly the correct position in the image. As SLAM methods track the camera in the first frame's coordinate system, they may drift due to wrong initialization or inaccuracies in the reconstructed model. The depth measurements are disturbed by lens and depth distortions, and for example, Kinect devices suffer from strong non-linear depth distortions as described in [ HKH12 ]. In SLAM methods, the measurement errors will eventually accumulate, which may cause the tracker to drift. Model-based approaches however solve the camera pose directly in the reference target's coordinate system and allow the camera pose estimate to "slide" to the correct result. Scene geometry also sets limitations on the performance of depth-based SLAM methods. In [ MIK12 ], it was found that with Kinect devices, the minimum size of object details in the reconstruction is approximately 10 mm, which also represent the minimum radius of curvature in the scene that can be captured. Thus, highly concave scenes and sharp edges may be problematic for depth-based SLAM. In model-based tracking, the reference CAD model is accurate and does not depend on the measurement accuracy or the object geometry. Thus, the tracking errors are distributed more evenly compared to SLAM.
The goal of model-based depth camera tracking is to estimate the pose of the camera relative to a target object of the real world at every time step by utilizing a reference model of the target in the process. We use a 3D CAD model of the target as a reference. The main idea of our approach is to construct a 3D point cloud from the latest incoming raw depth frame, and align it with a point cloud that we generate from the reference model using the sensor intrinsics and extrinsics from the previous time step. The incremental change in the sensor pose is then multiplied to the pose of the last time step. Figure 1 illustrates the principle. We utilize ICP for finding the transformation between the point clouds. The ICP implementation is a modified version of KinFu, an open source implementation of KinectFusion available in the PCL library [ RC11 ]. In the following we revise the method and detail the modifications we made to the original implementation. The block diagram of the method is shown in Figure 2.
Figure 1. Top left: The raw depth frame captured from the Kinect sensor. Top right: The artificial depth map rendered using Kinect's intrinsics and pose from the previous time step. Bottom left: The difference image of the rendered depth map and the raw depth frame before pose update. Bottom right: Corresponding difference image after the pose update. The colorbar units are in mm.
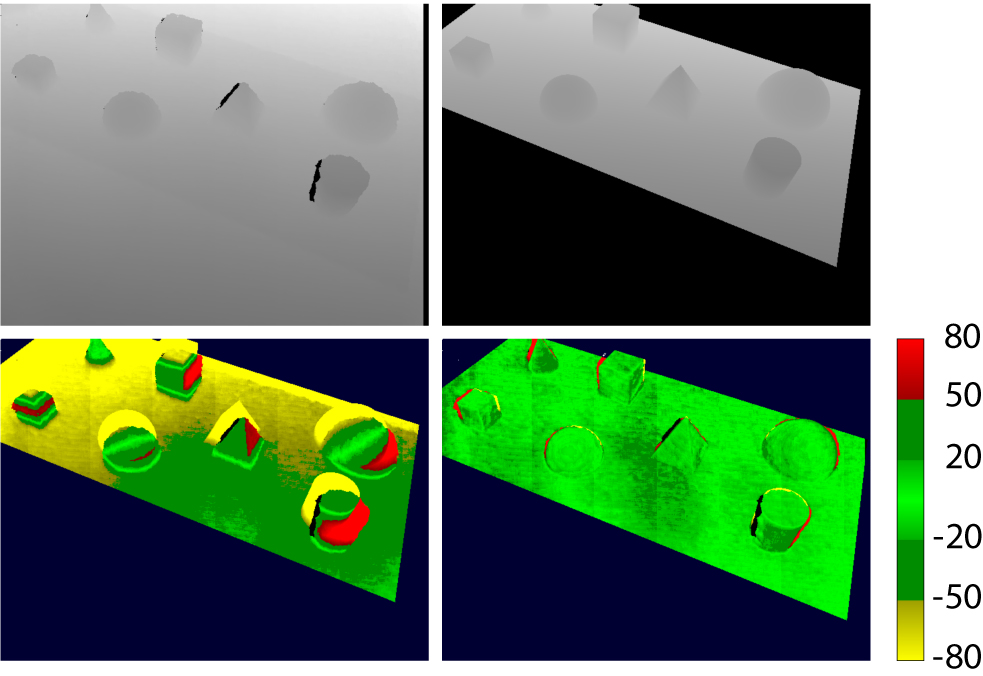
The depth camera is modeled with the conventional pinhole camera model. The senor intrinsics are denoted with K, which is a 3 x 3 upper triangular matrix having sensor's focal lengths and principal point. We denote the sensor extrinsics (pose) with P = [R|t], where R is the 3 x 3 camera orientation matrix and t is the camera position vector.
We denote a 3D point cloud with a set of 3D vertices V = {v1,v2,...} where vi = (xi,yi,zi)T , and similarly, we denote a set of point normal vectors with N = (n1,n2,...). To indicate the reference coordinate system of a point cloud, we use superscript g for global coordinate frame (i.e. reference model's coordinate system) and c for camera coordinate frame. Subscripts s and d refer to the source and to the destination point sets used in ICP, respectively.
The process starts by capturing a raw depth frame from the sensor and applying two optional steps: lens distortion correction and reducing the noise by filtering. For compensating the lens distortions, we use a standard polynomial lens distortion model. A bilateral filter is used to smooth the depth frame while keeping the depth discontinuities sharp. In the original implementation, bilateral filtering was used to prevent the noisy measurements from being accumulated in the reconstructed model, but the lens distortions were ignored. In our experiments, we evaluated the approach with both options turned on and off. The captured depth map is converted into a three-level image pyramid.
At each pyramid level l, the down scaled depth image
pixels are back projected to 3D space for constructing 3D
point clouds
 in the camera coordinate frame.
Additionally, normals
in the camera coordinate frame.
Additionally, normals
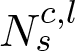 are calculated for the vertices.
The point clouds and normals are stored into arrays of the
same size as the depth image at current image pyramid
level.
are calculated for the vertices.
The point clouds and normals are stored into arrays of the
same size as the depth image at current image pyramid
level.
We render the reference CAD model from the previous
time step's camera view using the latest depth camera pose
estimate Pk-1
and the depth sensor intrinsics K in the
process. The frame size is set to the size of the raw depth
frames. We read the corresponding depth map from the
depth buffer, and construct a depth image pyramid
similarly to the raw depth maps. We construct 3D point
clouds
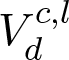 for each pyramid level l, and calculate the
corresponding normals
for each pyramid level l, and calculate the
corresponding normals
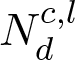 . Finally, we transform the
point cloud to the global coordinate system to obtain
. Finally, we transform the
point cloud to the global coordinate system to obtain
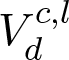 ,
and rotate the normals accordingly.
,
and rotate the normals accordingly.
We run the lens distortion compensation on the CPU, and as in the original implementation, the rest of the preprocessing steps are performed in the GPU using the CUDA language.
Figure 2. Block diagram of the model-based depth camera tracking approach. The change in the depth sensor pose is estimated by aligning the captured depth frame with the depth frame obtained by rendering the reference model with the previous time step's pose estimate. Lens distortion compensation and bilateral smoothing of the raw depth frame (marked with *) are optional steps in the processing pipeline.
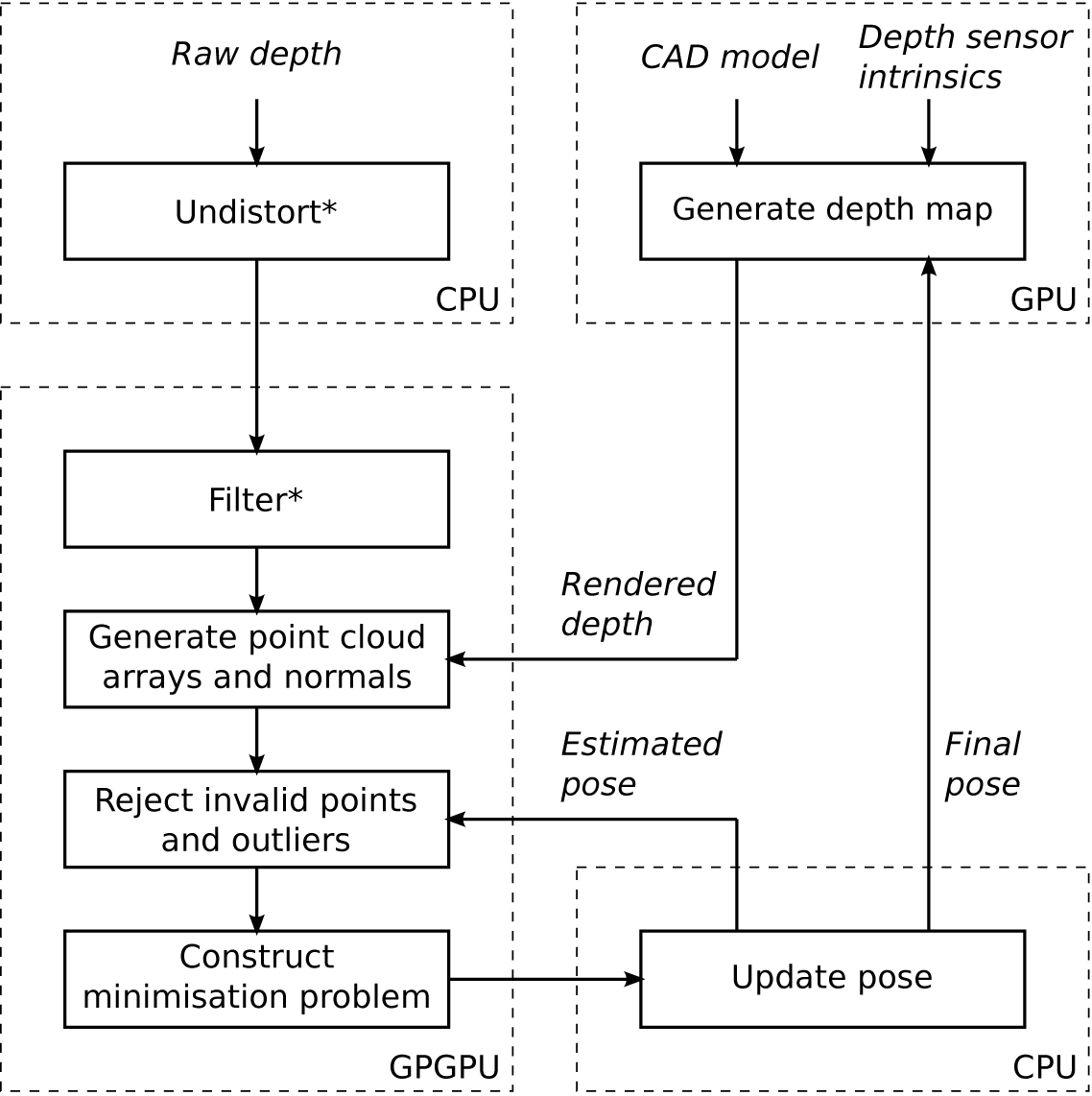
The change of the camera pose between two consecutive
time steps k-1 and k is estimated by finding the rigid
6-DoF transformation P' = [R'|t'] that aligns the source
point cloud
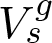 with the destination point cloud
with the destination point cloud
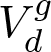 . The
procedure is done iteratively using ICP at different
pyramid levels, starting from the coarsest level and
proceeding to the full scale point clouds. At each ICP
iteration, the point cloud
. The
procedure is done iteratively using ICP at different
pyramid levels, starting from the coarsest level and
proceeding to the full scale point clouds. At each ICP
iteration, the point cloud
 is transformed to the world
frame with the latest estimate of Pk
, and the result
is transformed to the world
frame with the latest estimate of Pk
, and the result
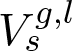 is
compared with the point cloud
is
compared with the point cloud
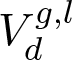 to evaluate the
alignment error. The error is minimized to get the
incremental change
to evaluate the
alignment error. The error is minimized to get the
incremental change
KinFu utilizes a point-to-plane error metric to compute
the cost of the difference between the point clouds. The
points of the source and destination point clouds are
matched to find a set of point pairs. For each point pair, the
distance between the source point and the correponding
destination point's tangent plane is calculated. Then the
difference between the point clouds is defined as the sum
of squared distances:
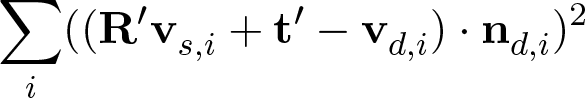 . (1)
. (1)
The rotation matrix R' is linearized around the previous
pose estimate to construct a linear least squares problem.
Assuming small incremental changes in the rotation, the
linear approximation of R' becomes
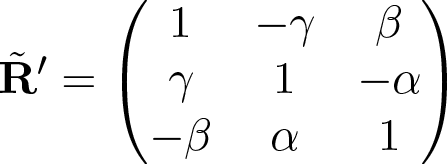 , (2)
, (2)
where α, β and γ are the rotations around x, y and z axes
respectively. Denoting r' = (α,β,γ)T
, the error can be
written as
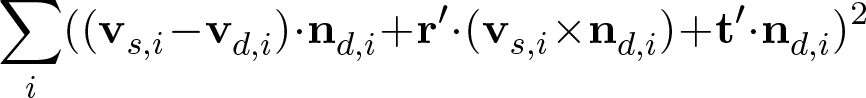 . (3)
. (3)
The minimization problem is solved by calculating the
partial derivatives of Equation 3 with respect to
the transformation parameters r' and t' and setting
them to zero. The equations are collected into a linear
system of the form Ax = b, where x consists of the
transformation parameters, b is the residual and A is a
6 x 6 symmetric matrix. The system is constructed in the
GPU, and solved using Cholesky decomposition in the
CPU.
To define the point pairs between the source and the
destination point clouds, KinFu utilizes projective data
association. At each ICP iteration, the points of
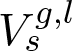 are
transformed to the camera coordinate system of the
previous time step, and projected to the image domain:
are
transformed to the camera coordinate system of the
previous time step, and projected to the image domain:
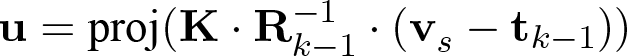 , (4)
, (4)
where
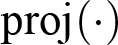 is the perspective projection including the
dehomogenization of the points. The set of tentative point
correspondences are then defined between the points of
is the perspective projection including the
dehomogenization of the points. The set of tentative point
correspondences are then defined between the points of
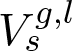 and the points of
and the points of
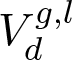 that correspond to the image
pixel coordinates u.
that correspond to the image
pixel coordinates u.
The tentative point correspondences are checked for outliers by calculating their Euclidean distance and angle between their normal vectors. If the points are too distant from each other, or the angle is too large, the point pair is ignored from the ICP update. In our experiments, we used a 50 mm threshold for the distance and a 20 degree threshold for the angle. The Kinect cannot produce range measurements from some materials like reflective surfaces, under heavy sunlight, outside its operating range and from occluded surfaces, and such source points are ignored too. Furthermore, we ignore destination points that have infinite depth value, i.e. the depth map pixels where no object points are projected when rendering the depth map.
The proposed tracking approach simplifies the use of 3D CAD models in visual tracking since there is no need for extracting and matching interest points or other cues or features. The only requirement is that a depth map from the desired camera view can be rendered effectively, and retrieved from the depth buffer. Complex CAD models can be effectively rendered using commonly available tools. In our experiments, we used OpenSG to manipulate and render the model.
We evaluated the accuracy, stability and robustness of the proposed approach by comparing the tracking results to ground truth in three different tracking scenarios and with six datasets. We also compared the results to KinFu and to the edge-based monocular method presented in [ WWS07 ]. Additionally, we compared the computational time required for sensor pose update between the different tracking methods.
In this section, we describe the data collection procedure, the error metrics that we used to evaluate the results, and the datasets that we collected from the experiments. For simplicity, we refer to the proposed approach as "model-based method", and the 2D model based approach as "edge-based method".
Figure 3. The reference CAD models used to evaluate the proposed approach. Top and bottom left: Target 1 consist of several convex objects attached to a common plane. The model is partially textured and partially plain white. Middle: Target 2 is a car's dashboard. The model differs from its real counterpart from the steering wheel, gear stick as well as the middle console. Right: Target 3 does not have geometry in vertical dimension and the ICP based approach is not fully constrained by the target.

We conducted the experiments with offline data that we captured from three test objects using the Kinect depth sensor. For each data sequence, we captured 500 depth frames at a resolution of 640 x 480 pixels and frame rate of 10 FPS. In addition to depth frames, we captured the RGB frames for evaluating the performance of the edge-based method. To collect the ground truth camera trajectories, we attached the sensor to a Faro measurement arm, and solved the hand-eye calibration of the system as described in [ KHW14 ]. For KinFu, we set the reconstruction volume to the size of each target's bounding box and aligned it accordingly. The model-based method was run without lens distortion compensation and bilateral filtering, and we used L = {10,5,4} ICP iterations. We also experimented with other settings, and the results are discussed in Section 5.5. The test targets and the corresponding 3D CAD models are shown in Figure 3.
For the evaluation runs, we initialized the trackers to the ground truth pose, and let them run as long as the estimated position and orientation remained within the predefined limits. Otherwise the tracker was considered to be drifting, and its pose was reset back to the ground truth. The tracker's pose was reset if the absolute error between the estimated position and the ground truth was more that 20 cm, or if the angle difference was more than 10 degrees.
Due to lens and depth distortions as well as noise in the depth measurements, the hand-eye calibration between the Faro measurement arm and the Kinect device is inaccurate. The result depends on the calibration data, and the calibration obtained with close range measurements may give inaccurate results with long range data and vice versa. Thus, we estimated the isometric transformation between the resulting trajectories and ground truth, and generated a corrected ground truth trajectory for each sequence individually. For the final results, we repeated the tests using the corrected ground truth trajectories as reference.
We measured the accuracy of the trackers by calculating the mean of absolute differences between the estimated sensor positions and the (corrected) ground truth over the test sequences. Similarly, we measured the error in orientation, and calculated the mean of absolute differences between the angles. We define the angle error as the angle difference between the quaternion representations of the orientations. We calculated the corresponding standard deviations for evaluating the jitter, and used the number of required tracker resets as a measure for robustness.
In AR applications, it is essential that the rendered model is aligned accurately with the view and the reprojection error is typically used to measure the accuracy of vision-based trackers. In 2D analysis, the reprojection error is calculated by summing up the squared differences between the observed and reprojected model points in the image domain after the camera pose update. We use a similar approach in 3D, and calculate the differences between the observed and rendered depth maps. We define two error metrics using the depth: error metric A and error metric B.
The error metric A is the difference between the depth map rendered using the ground truth pose and the depth map rendered using the estimated pose. This measures the absolute accuracy of the tracker. It takes into account the range measurement errors, but cannot distinguish the inaccuracies in hand-eye calibration from the real positioning errors. The error metric can also be used to evaluate the monocular edge-based method. The error metric is defined for the pixels where either the first or the second input depth map has a valid value.
The error metric B is the difference between the depth map rendered using the estimated pose and the raw depth map captured from the camera. The error metric is similar to the 2D reprojection error, and it describes how well the model is aligned with the captured depth images. The lens distortions and errors in range measurements may cause inaccurate pose estimation, for which the error metric is not sensitive. However, it is important for AR applications as it measures how accurately the virtual objects can be overlaid over the (depth) images. The error metric is defined only for the pixels where both input depth maps have valid values.
The error metrics are illustrated in Figure 4. For the evaluation, we calculated difference images using the error metrics A and B, and visualized the results using histograms. Each histogram bin contains the number of positive and negative differences at a bin size of 2 mm. We normalized the histograms so that the maximum value of the bins was set to one, and the other bins were scaled respectively. To emphasize the distribution of the errors, we ignored coarse outliers (absolute differences over 50 mm) from the histograms, and calculated their ratio in difference images to tables.
Figure 4. 3D error metrics used in the evaluation. Left: The difference between the depth map rendered using the ground truth pose and the depth map rendered using the estimated pose (error metric A). Right: The difference between the depth map rendered with the estimated pose and the raw depth frame (error metric B). The colorbar units are in mm.
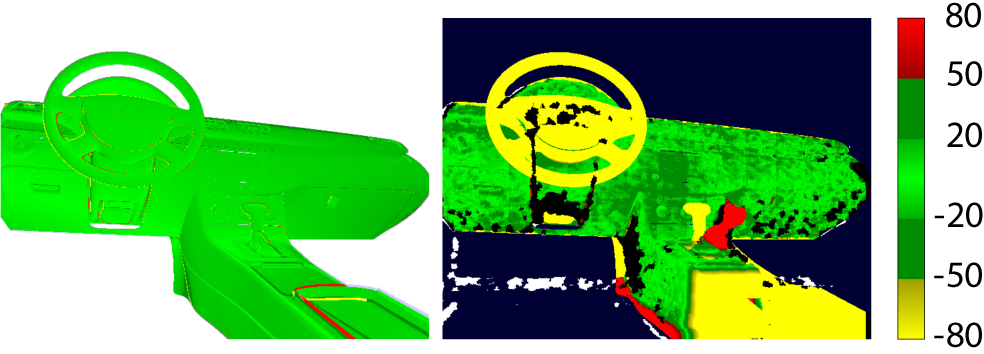
We evaluated the computational load of different approaches by measuring the time to perform the main steps required for the pose update. The evaluation was conducted with a desktop computer (Intel i7-870 3 GHz with Nvidia GTS 450 graphics card) and with a laptop (Intel i7-3740QM 2.7 GHz with Nvidia NVS 5200M). The results are shown in Table 1. The timing results for model-based approach with other parameterizations are discussed in section 5.5.
Table 1. Timing results for camera pose update with different methods. Model-based tracker and KinFu were evaluated with laptop (Intel i7-3740QM 2.7 GHz with Nvidia NVS 5200M) and desktop PC (Intel i7-870 3 GHz with Nvidia GTS 450). The edge-based method was evaluated with the laptop only.
|
Processing step |
Timing |
|
Model-based method |
|
|
Constructing the artificial depth map |
12 % |
|
Preprocessing the raw depth |
11 % |
|
Preprocessing the artificial depth |
11 % |
|
Updating the pose |
66 % |
|
Total, desktop PC |
60 ms |
|
Total, laptop PC |
160 ms |
|
KinFu |
|
|
Preprocessing the raw depth |
10 % |
|
Updating the pose |
50 % |
|
Volume integration |
35 % |
|
Raycasting the artificial depth |
5 % |
|
Total, desktop PC |
130 ms |
|
Total, laptop PC |
240 ms |
|
Edge-based method |
|
|
Edge shader and sampling |
50 % |
|
Finding point correspondences |
29 % |
|
Updating the pose |
21 % |
|
Total, laptop PC |
15 ms |
Target 1 has seven objects attached to a common plane: two pyramids, two half spheres and two boxes. The size of the plane is approximately 1 x 1.5 m, and the objects are from 10 to 12 cm in height. The target has variance in shape in every dimension, and the objects have sharp edges and corners. Thus, it is constraining both the depth-based as well as the monocular edge-based tracking methods. Furthermore, the object has textured and non-textured parts. The surface material gives a good response to the Kinect, but in some experiments, the camera was moved very close to the target and part of the depth measurements were lost (the minimum distance for range measurements with the Kinect is approximately 40 cm). We captured three sequences from Target 1 as follows:
Sequence 1.1
The sequence starts such that the whole
target is in camera view. The camera is moved
from side to side four times so that the optical
center is directed to the center of the target. In
the last part of the sequence, the camera is moved
closer to the target, and the range measurements
are partially lost.
Sequence 1.2
The sequence starts on the right side of
the target so that approximately half of the target
is visible. The camera is moved closer to the
target and the range measurements are partially
lost. Finally, the camera is moved from side to
side twice.
Sequence 1.3
The sequence starts from the left side
of the target so that approximately half of the target is visible. The camera is moved closer to
the target and is rotated from side to side (yaw
angle). Finally, the camera is moved back and
forth. During the sequence, the camera is moved
close to the target, and the range measurements
are partially lost.
Target 2 is a car dashboard of regular size and material. Compared to the reference CAD model, the target does not have the steering wheel and the gear stick and the middle console are different. Similarly to Target 1, Target 2 has variance in shape in every dimension as well as relatively sharp edges. We captured two sequences from Target 2 as follows:
Sequence 2.1
The sequence starts such that the
dashboard is completely in the camera view. The
camera is moved closer to the left side, and then
around the gear stick to the right side of the target.
During the sequence, there is no notable change
in roll or pitch angles in the camera orientation.
Sequence 2.2
The sequence starts such that the
camera is pointing to the right side of the target
and is relatively close in distance. The camera
is moved around the gear stick so that the target
fills the camera view almost completely. Then,
the camera is moved back to the right side and
pulled back so that the whole target becomes
visible in the camera. During the sequence, there
is no notable change in roll or pitch angles in the
camera orientation.
Target 3 is a plastic object with a matte, light red surface. The shape of the object is smooth and curved, and it has no vertical changes in geometry. Thus, the ICP is not constrained in every dimension. The target is also challenging for the 2D edge-based tracker, since the object's outer contour is the only edge to be used in registration process. We captured the following sequence from Target 3:
Sequence 3.1
The sequence starts from the right side
such that the target is completely in the camera
view and the camera is directed towards the
center of the target. The camera is moved to the
left side so that the target is kept completely in
the camera view, and the distance to the target
remains constant. During the sequence, there is
no notable change in roll or pitch angles in the
camera orientation.
All trackers perform robustly in Sequence 1.1. Figure 5 shows the absolute errors of the trajectories (positions) given by the different methods. Neither model-based nor KinFu trackers are reset during the test, and the monocular edge-based tracker is reset twice. The absolute translation error of the model-based tracker remains mostly under 20 mm. Compared to the model-based method, the edge-based tracker is on average more accurate but suffers more from jitter and occasional drifting. The translation error of KinFu is small in the beginning but increases as the tracker proceeds, and reaches a maximum of approximately 40 mm near frame 250. The mean error of the model-based tracker is 14.4 mm and the standard deviation 5.9 mm (Table 2). The corresponding values for KinFu and edge-based trackers are 20.2 mm (10.7 mm) and 18.7 mm (26.4 mm) respectively. The angle errors behave similarly compared to the translation errors and the rest of the results are shown in Table 3.
Figure 5. Absolute error of the estimated camera position using different tracking methods. Red curves refer to the model-based tracker, green to KinFu and blue to the edge-based method. Vertical lines denote tracker resets. Y-axis indicates the error value at each frame in mm, and x-axis is the frame number.
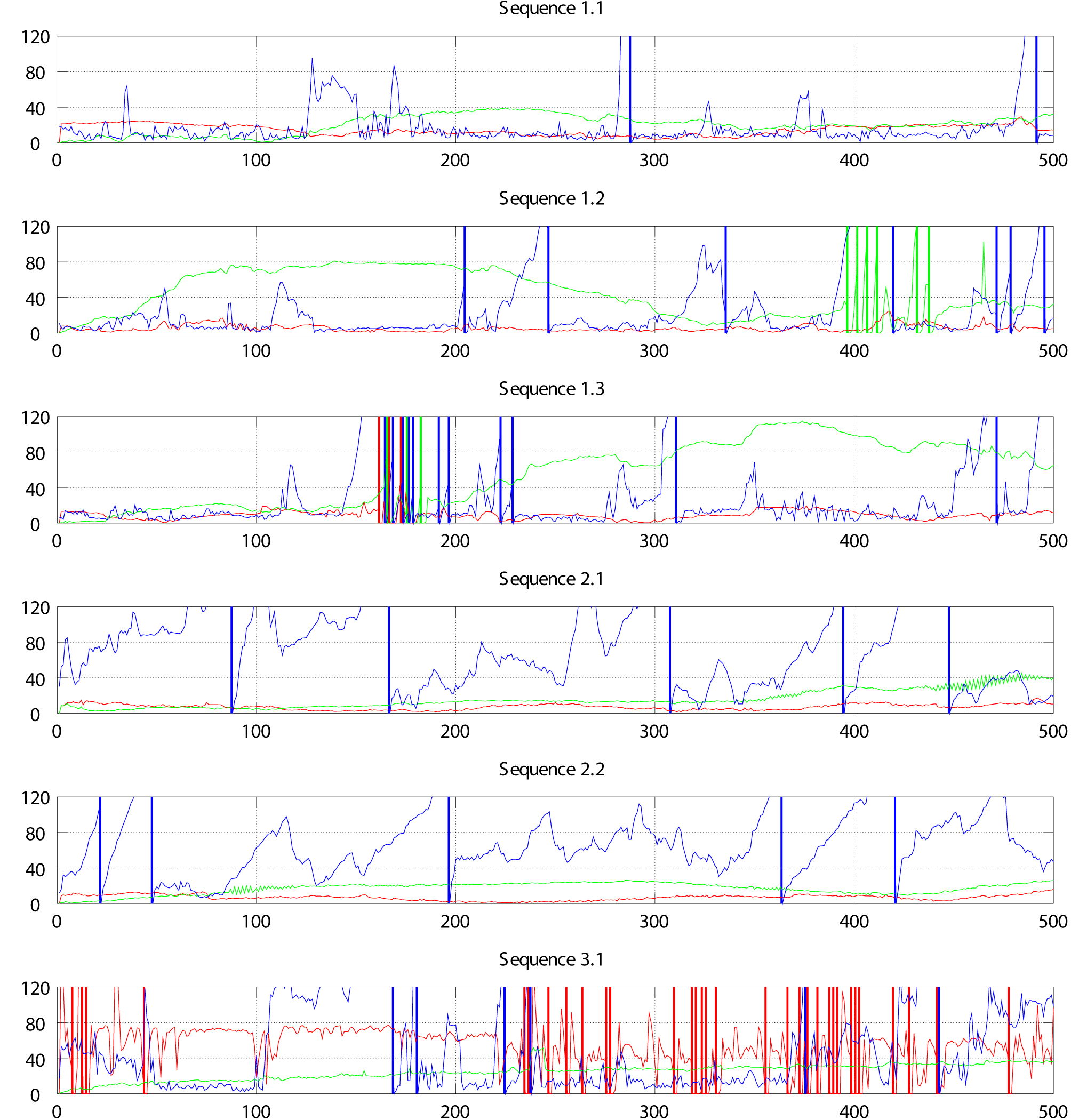
Figure 6. The distribution of the errors computed using the error metric A. The coarse outliers (absolute value more than 50 mm) are ignored. The histograms are normalized so that their maximum values are set to one, and the other values are scaled respectively.
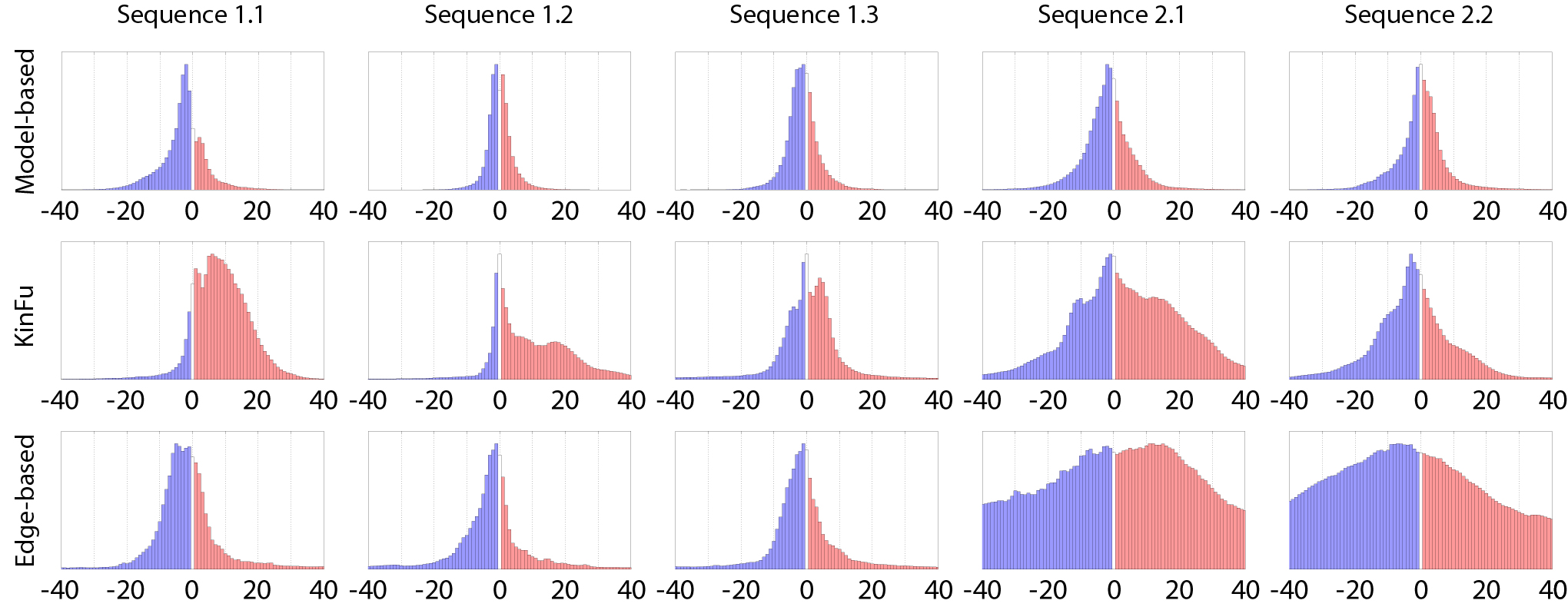
Figure 7. The distribution of the errors computed using the error metric B. The coarse outliers (absolute value more than 50 mm) are ignored. The histograms are normalized so that their maximum values are set to one, and the other values are scaled respectively.
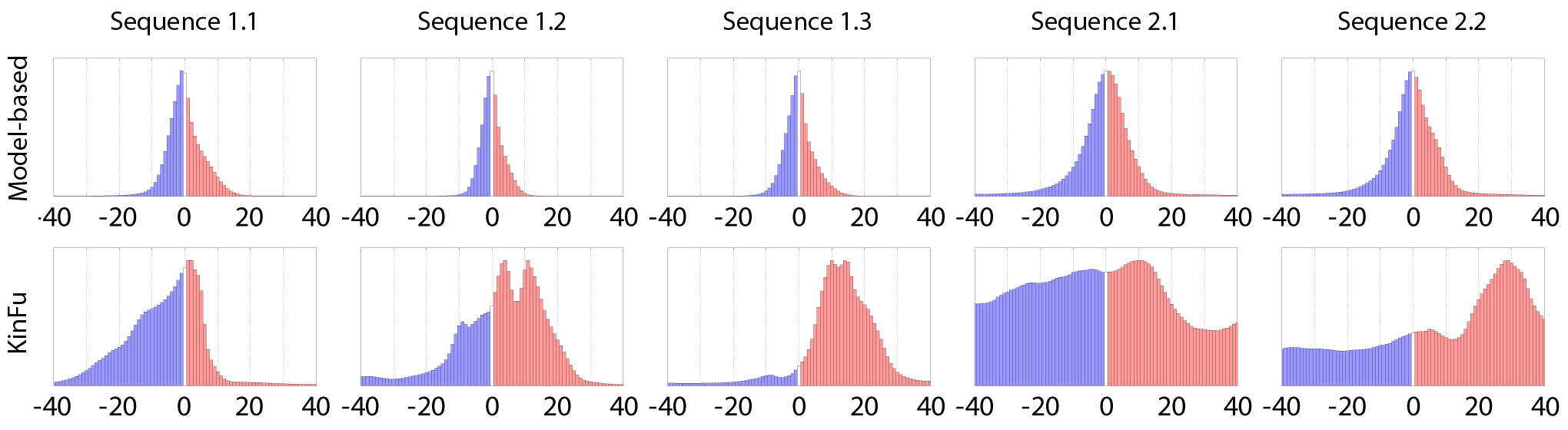
The distribution of the reprojection errors computed using the error metric A are shown in Figure 6. The error distribution of each tracker is symmetric. The model-based and the edge-based methods slightly overestimate the distance to the target, and the result of KinFu is opposite which on average underestimates the distance. The model-based approach has the narrowest and KinFu the broadest distribution of errors. Table 4 shows the ratio of coarse outliers (absolute differences over 50 mm) in the difference images. The ratio of outliers for the model-based tracker and KinFu are similar (4.6 % and 4.2 % respectively), and for the edge-based method 7.3 %.
To evaluate how accurately virtual data could be registered with raw depth video, we calculated the reprojection errors for the model-based method and KinFu using the error metric B. The error histograms in Figure 7 show that the errors of the model-based tracker are symmetrically distributed around zero. The ratio of the coarse outliers is 1.1 % (Table 5). The error distribution of the KinFu tracker is centered around +6 mm, and the shape is skewed towards positive values. The ratio of outliers is 5.3 %.
Compared to Sequence 1.1, the model-based tracker performs more accurately in Sequences 1.2 and 1.3. In Sequence 1.2, the mean absolute error of the position is 5.3 mm and standard deviation 3.8 mm. In Sequence 1.3, the corresponding values are 9.0 mm and 5.0 mm respectively. The tracker is reset three times during Sequence 1.3 and can track Sequence 1.2 completely without resets. In Sequences 1.2 and 1.3, the camera is moved closer to the target and the depth data is partially lost.
Table 2. Mean absolute errors and standard deviations of estimated sensor position (in mm).
|
|
Model-based |
KinFu |
Edge-based |
|
Seq 1.1 |
14.4 (5.9) |
20.2 (10.7) |
18.7 (26.4) |
|
Seq 1.2 |
5.3 (3.8) |
43.4 (26.3) |
26.0 (37.0) |
|
Seq 1.3 |
9.0 (5.0) |
54.1 (36.0) |
26.4 (38.6) |
|
Seq 2.1 |
7.2 (3.2) |
15.7 (10.4) |
75.6 (47.0) |
|
Seq 2.2 |
6.8 (3.2) |
16.8 (6.5) |
67.3 (34.8) |
|
Seq 3.1 |
50.5 (28.4) |
24.5 (8.8) |
50.4 (47.6) |
Table 3. Mean absolute errors and standard deviations of estimated sensor orientation (in degrees).
|
|
Model-based |
KinFu |
Edge-based |
|
Seq 1.1 |
0.6 (0.3) |
1.0 (0.5) |
1.0 (1.2) |
|
Seq 1.2 |
0.6 (0.4) |
2.7 (1.6) |
1.8 (2.3) |
|
Seq 1.3 |
0.5 (0.5) |
2.6 (1.5) |
1.6 (1.9) |
|
Seq 2.1 |
0.5 (0.3) |
0.9 (0.6) |
3.5 (2.0) |
|
Seq 2.2 |
0.5 (0.2) |
1.0 (0.5) |
4.6 (2.0) |
|
Seq 3.1 |
1.8 (1.2) |
1.4 (0.5) |
3.0 (2.8) |
Presumably KinFu suffers from the incomplete depth data, and the mean absolute error and the standard deviation in Sequence 1.2 are more than doubled compared to Sequence 1.1, and almost tripled in Sequence 1.3. The number of resets of KinFu are six and three in Sequences 1.2 and 1.3 respectively. In Sequence 1.2, the resets occur close to the frame 400 where the camera is close to the target and approximately half of the depth pixels are lost. The accuracy of the edge-based method decreases slightly too. It is reset seven times during Sequence 1.2 and eleven times in Sequence 1.3. In Sequence 1.3, between the frames 150 and 200, all of the trackers are reset multiple times. During that time interval, the camera is moved close to the target and approximately half of the depth pixels are lost. Additionally, the camera is rotated relatively fast around its yaw axis. Tables 2 and 3 show the rest of the results.
The distribution of the reprojection errors in Figures 6 and 7 are similar to Sequence 1.1. Also, the ratio of outliers in Tables 4 and 5 are consistent with the tracking errors. Figure 8 has example images of the evaluation process in Sequence 1.2. As shown in the images, the depth data is incomplete and partially missing since the sensor is closer to the target than its minimum sensing range. Both model-based approaches are able to maintain the tracks accurately, but the drift of KinFu is clearly visible.
The CAD model of Target 2 differs from its real counterpart, and there are coarse outliers in the depth data of Sequences 2.1 and 2.2. The translation errors in Figure 5 show that both the model-based tracker and KinFu perform robustly, and the trackers are not reset during the tests. The edge-based method suffers from drift and it is reset five times in both experiments. Tables 2 and 3 as well as Figure 5 show that the accuracy of the model-based method is comparable to the first three experiments, and that the approach is the most accurate from the methods.
Figure 8. Tracker performance evaluation examples in different scenarios. Top row images are from the frame 150 of Sequence 1.2 and bottom row images are from the frame 250 of Sequence 2.1. Top row images 1-2 (from the left): Results of the model-based method calculated with the 3D error metric A and B. Top row images 3-4: Corresponding results for KinFu. Top row image 5: The result of the edge-based method calculated with the 3D error metric A. Bottom row images are ordered similarly to the top row. The colorbar units are in mm.
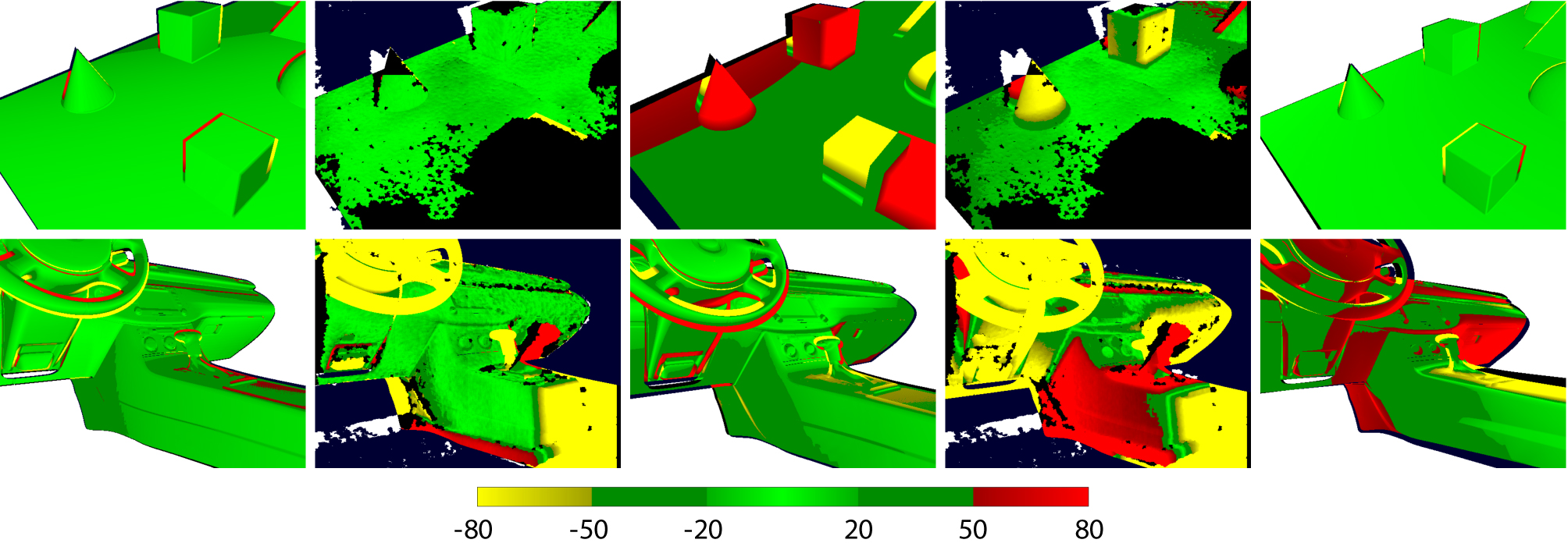
Table 4. The ratio of outliers in difference images calculated using the error metric A.
|
|
Model-based |
KinFu |
Edge-based |
|
Seq 1.1 |
4.6 % |
4.2 % |
7.3 % |
|
Seq 1.2 |
1.9 % |
11.6 % |
9.4 % |
|
Seq 1.3 |
3.1 % |
11.6 % |
11.0 % |
|
Seq 2.1 |
4.4 % |
13.9 % |
44.2 % |
|
Seq 2.2 |
4.8 % |
8.3 % |
41.7 % |
|
Seq 3.1 |
25.8 % |
5.2 % |
18.4 % |
Table 5. The ratio of outliers in difference images calculated with the error metric B.
|
|
Model-based |
KinFu |
|
Seq 1.1 |
1.1 % |
5.3 % |
|
Seq 1.2 |
0.9 % |
5.5 % |
|
Seq 1.3 |
0.7 % |
11.6 % |
|
Seq 2.1 |
35.9 % |
58.3 % |
|
Seq 2.2 |
34.9 % |
47.2 % |
|
Seq 3.1 |
8.4 % |
5.2 % |
The error histograms based on the error metric A are shown in Figure 6. The results of the model-based tracker are similar to the first three experiments, and the errors are distributed symmetrically with close to zero mean. The error distributions of KinFu and the edge-based method are more wide spread and the drift of the edge-based method is especially visible. For the model-based tracker and KinFu, the ratio of outliers in reprojection errors are similar to Target 1, and for the edge-based method the ratio clearly increases. The error histograms based on the error metric B show that the model-based tracker performs consistently, and that the reprojected model was aligned to the captured depth frames without bias. The KinFu tracker has more a widespread error distribution. Table 5 shows that there are more coarse outliers in the results of KinFu as well. Note, that due to differences between the reference CAD model and its real counterpart, the number of outliers is relatively high in both methods.
The images in Figure 8 show tracking examples from Sequence 2.1. The difference images computed using the error metric B show that the model-based tracker aligns the observed depth maps accurately with the rendered model, and the real differences are clearly distinguishable from the images. With KinFu, the real differences and positioning errors are mixed. The error metric A shows that the model-based approach is close to ground truth and major errors are present only around the edges of the target.
Target 3 does not constrain the ICP in the vertical dimension and the model-based tracker fails to track the camera. Figure 5 shows that the model-based tracker drifts immediately after the initial reset, and that there are only a few sections in the experiment where the tracker is stable (but still off from the ground truth trajectory). Since the model-based tracker was drifting, we did not compensate the bias in the hand-eye calibration for any of the methods (see Section 4.1). The edge-based tracker performs better and it is able to track the camera for most of the frames, although it was reset seven times during the test. KinFu performs equally well compared to the previous experiments, and it is able to track the camera over the whole sequence without significant drift. The result is unexpected since KinFu's camera pose estimation is based on the ICP. We assume that noisy measurements are accumulated to the 3D reconstruction, and these inaccuracies in the model are constraining ICP in the vertical dimension.
In AR applications, it is essential that the tracking system performs without lag and as close to real-time frame rates as possible. When a more computationally intensive method is used for the tracking, a lower frame rate is achieved and the wider baseline between successive frames needs to be matched in a pose update. We evaluated the effect of lens distortions, raw data filtering and the number of ICP iterations separately to the accuracy in Sequences 1.1 and 2.1. Each of them increases the computational time and are optional. Table 6 shows the results. Compared to the results shown in Table 2 (lens distortion compensation off, bilateral filtering off, number of ICP iterations set to L = {10,5,4}), it can be seen that the bilateral filtering step does not improve the accuracy, and can be ignored for the model-based tracking approach. Lens distortion compensation improved the accuracy slightly in Sequence 1.1, but improves the accuracy by approximately 26 % in Sequence 2.1. Reducing the number of iterations in ICP does not have notable change in Sequence 1.1 and decreases the accuracy by 7 % in Sequence 2.1. With the laptop PC, the lens distortion compensation (computed in CPU) takes approximately 7 ms and the tracker with ICP iterations L = {1,1,1} 50 ms versus 160 ms with L = {10,5,4}. Bilateral filtering (computed in GPU) does not add notable computational load.
Figure 9. The spatial distribution of the positive (left image) and negative (right image) depth differences between the depth map rendered with the pose estimate given by model-based tracker and the raw depth map captured from the camera (error metric B). The images were constructed by calculating the mean errors for every pixel over Sequence 1.3. To emphasize the sensor inaccuracies, the results were thresholded to ∓10 mm. The error distribution is similar compared to the image presented in [ HKH12 ]. The colorbar units are in mm.
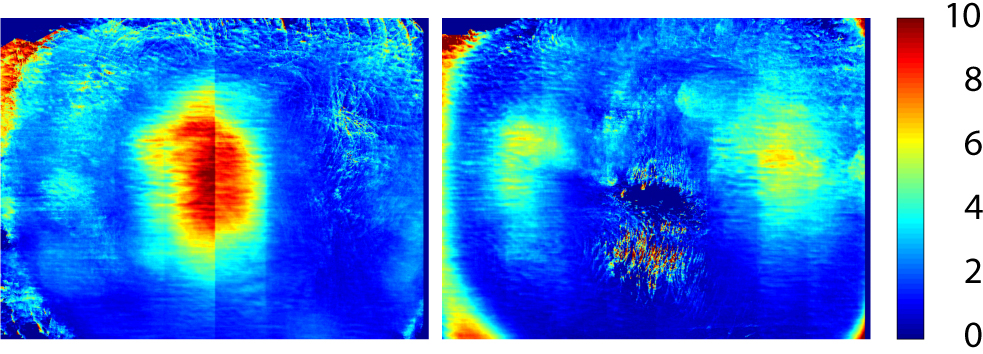
In addition to noise and lens distortions, the Kinect suffers from depth distortions that depend on the measured range and that are unevenly distributed in the image domain [ HKH12 ]. We calculated the mean positive and negative residual images over Sequence 1.3 using the error metric B and the model-based tracker. We thresholded the images to ∓10 mm to emphasize the sensor depth measurement errors and to deduct the pose estimation errors. Figure 9 shows the error images, which are similar to the observations in [ HKH12 ]. We did not evaluate the effect of the range measurement errors quantitatively, but in applications that require very precise tracking, the compensation of such errors should be considered.
Table 6. Mean absolute error and standard deviation of the estimated sensor position with different tracking options using the model-based tracker. "Filtered" refers to experiments where the bilateral filtering of the raw depth frames was turned on, "Undistorted" refers to experiments with (spatial) lens distortion compensation and "Iteration test" to experiments where the ICP was run only once at each pyramid level.
|
|
Filtered |
Undistorted |
Iteration test |
|
Seq 1.1 |
14.5 (6.0) |
13.9 (5.4) |
14.5 (5.8) |
|
Seq 2.1 |
7.2 (3.3) |
5.3 (2.6) |
7.7 (3.9) |
We proposed a method for real-time CAD model-based depth camera tracking that uses ICP for pose update. We evaluated the method with three real life reference targets and with six datasets, and compared the results to depth-based SLAM, to a 2D edge-based method and to the ground truth.
The results show that the method is more robust compared to the 2D edge-based method and suffers less from jitter. Compared to depth-based SLAM, the method is more accurate and has less drift. Despite incomplete range measurements, noise, and inaccuracies in the Kinect depth measurements, the 3D reprojection errors are distributed evenly and are close to zero mean. For applications that require minimal lag and fast frame rates, it seems sufficient to run the IPC iterations only once for each pyramid level. This does not affect to the accuracy or jitter, but speeds up the processing time significantly. In our experiments, filtering the raw depth frames did not improve the tracking accuracy, but for applications that require very precise tracking, the lens distortions should be compensated. Additionally, the Kinect sensor suffers from depth measurement errors. The distribution of the errors in the image domain is complex, and a depth camera model that compensates the errors pixel-wise (e.g. [ HKH12 ]) should be considered.
The ICP may not converge to the global optimum if the target object does not have enough geometrical constraints (the problem has been discussed e.g. in [ GIRL03 ]). This leads to wrong pose estimates and drift, and limits the use of the method to objects that have variance in shape in all three dimensions. However, in our experiments, KinFu was more stable with such object and did not drift during the tests. The exact reason for this behavior is unclear to us, but we assume that the inaccuracies and noise in range measurements are accumulated to the reference model constraining the tracker.
We excluded the tracker initialization from this paper. In practical applications, the automated initialization is required, and to initialize the camera pose one may apply methods developed for RGB-D based 3D object detection (e.g. [ HLI13 ]) or methods that rely on depth information only (e.g. [ SX14 ]). As the ICP aligns the model and the raw depth frames in a common coordinate system, the model-based method (as well as the edge-based method) is forgiving to inaccurate initialization. The maximum acceptable pose error in the initialization stage depends on the reference model geometry. Detailed surfaces with a lot of repetitive geometry may guide the ICP to local minimum, but smooth and dominant structures allow the tracker to slide towards the correct pose.
Although we did not evaluate the requirements for the size of the reference model's appearance in the camera view, some limitations can be considered. The projection of small or distant objects occupy relatively small proportion of the depth frames, and the relative noise level of the depth measurements increases. Thus, the geometrical constraints may become insufficient for successful camera pose estimation. Additionally, if the camera is moved fast or rotated quickly between the consecutive frames, the initial camera pose from the previous time step may differ significantly from the current pose. Thus, small or distant objects may be treated completely as outliers, and the pose update would fail. The exact requirements for the reference model's visual extent in the camera view depend on the size of the objects and how the camera is moved. Similar methods as suggested for automatic initialization could be used in background process to reinitialize the pose whenever it has been lost.
With the proposed approach, virtually any CAD model can be used for depth camera tracking. It is required that the model can be efficiently rendered from the desired camera pose and that the corresponding depth map can be retrieved from the depth buffer. The models that do not have variance in shape in every dimension do not completely constrain the ICP which may lead to drift. We envision that the method could be improved by making partial 3D shape reconstructions online, and appending the results to the CAD model for more constraining geometry. Other suggestion for improvement is to complete the method with an edge-based approach to prevent the tracker from drifting. For example, a 3D cube fully constraints the ICP as long as three faces are seen by the camera. But if the camera is moved so that only one face is visible, only the distance to the model is constrained. However, the edge information would be still constraining the camera pose.
The authors would like to thank professor Tapio Takala from Aalto University, Finland for valuable comments, and Alain Boyer from VTT Technical Research Centre of Finland for language revision.
[AZ95] Robust object tracking Asian Conference on Computer Vision, 1995 , pp. 58—61 9810071884
[Azu97] A survey of augmented reality Presence: Teleoperators and Virtual Environments, 1997 4 355—385 DOI 10.1162/pres.1997.6.4.355, 1054-7460
[BBS07] Real-time vision-based tracking and reconstruction, Journal of Real-Time Image Processing, 2007 2 161—175 DOI 10.1007/s11554-007-0034-0, 1861-8200
[BPS05] Real-time 3D camera tracking for industrial augmented reality applications WSCG 2005: Full Papers: The 13-th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision 2005 in co-operation with Eurographics: University of West Bohemia, Plzen, Czech Republic, (Václav Skala ed.), 2005 pp. 47—54 HDL 11025/10951, 80-903100-7-9
[BSK13] Real-Time camera tracking and 3D reconstruction using signed distance functions Robotics: Science and Systems (RSS) Conference 2013, 2013 , 978-981-07-3937-9
[CC13] RGB-D object tracking: a particle filter approach on GPU 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2013 pp. 1084—1091 DOI 10.1109/IROS.2013.6696485.
[DC02] Real-time visual tracking of complex structures IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002 7 932—946 DOI 10.1109/TPAMI.2002.1017620, 0162-8828
[DRMS07] MonoSLAM: Real-time single camera SLAM IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007 6 1052—1067 DOI 10.1109/TPAMI.2007.1049, 0162-8828
[GIRL03] Geometrically Stable Sampling for the ICP Algorithm Fourth International Conference on 3-D Digital Imaging and Modeling 3DIM, 2003 pp. 260—267 DOI 10.1109/IM.2003.1240258, 0-7695-1991-1
[GRV13] Metrological evaluation of Microsoft Kinect and Asus Xtion sensors Measurement, 2013 6 1800—1806 DOI 10.1016/j.measurement.2013.01.011, 0263-2241
[Har93] Tracking with rigid models Active vision, (Andrew Blake Alan Yuille eds.), 1993 MIT Press pp. 59—73 0-262-02351-2
[HF11] Exploring the benefits of augmented reality documentation for maintenance and repair IEEE Transactions on Visualization and Computer Graphics, 2011 10 1355—1368 DOI 10.1109/TVCG.2010.245, 1077-2626
[HKH12] Joint depth and color camera calibration with distortion correction IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012 10 2058—2064 DOI 10.1109/TPAMI.2012.125, 0162-8828
[HLCH12] Time of Flight Cameras: Principles, Methods, and Applications 2012 Springer London isbn 978-1-4471-4658-2, DOI 10.1007/978-1-4471-4658-2.
[HLI13] Model Based Training, Detection and Pose Estimation of Texture-Less 3D Objects in Heavily Cluttered Scenes Computer Vision - ACCV 2012: 11th Asian Conference on Computer Vision, Daejeon, Korea, November 5-9, 2012, Revised Selected Papers, (Kyoung Mu Lee Yasuyuki Matsushita James M. Rehg Zhanyi Hu eds.), 2013 Springer Berlin , pp. 548—562 DOI 10.1007/978-3-642-37331-2_42, 978-3-642-37330-5
[KBKF13] Towards precise real-time 3D difference detection for industrial applications Computers in Industry, 2013 9 1115—1128 DOI 10.1016/j.compind.2013.04.004, 0166-3615
[KHW14] Hand-eye calibration with a depth camera: 2D or 3D? 2014 International Conference on Computer Vision Theory and Applications (VISAPP), 2014 IEEE pp. 481—489, URL ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=7295121.
[KM06] Full-3D Edge Tracking with a Particle Filter Proceedings of the British Machine Vision Conference, (Mike Chantler Bob Fisher Manuel Trucco eds.), 2006 BMVA Press pp. 114.1-114.10 DOI 10.5244/C.20.114, 1-901725-32-4
[KM07] Parallel tracking and mapping for small AR workspaces 6th IEEE and ACM International Symposium on Mixed and Augmented Reality ISMAR 2007, 2007 pp. 225—234 DOI 10.1109/ISMAR.2007.4538852, 978-1-4244-1749-0
[LF05] Monocular model-based 3D tracking of rigid objects Foundations and Trends in Computer Graphics and Vision, 2005 1 1—89 DOI 10.1561/0600000001, 1572-2740
[MF01] VideoOrbits on eye tap devices for deliberately diminished reality or altering the visual perception of rigid planar patches of a real world scene International Symposium on Mixed Reality (ISMR2001), 2001 pp. 48—55.
[MIK12] When can we use KinectFusion for ground truth acquisition?, Workshop on Color-Depth Camera Fusion in Robotics, IEEE/RSJ International Conference on Intelligent Robots and Systems, 2012.
[NIH11] KinectFusion: real-time dense surface mapping and tracking 10th IEEE International Symposium on Mixed and Augmented Reality (ISMAR), 2011 IEEE pp. 127—136 DOI 10.1109/ISMAR.2011.6092378, 978-1-4577-2183-0
[PLW11] Texture-less object tracking with online training using an RGB-D camera 10th IEEE International Symposium on Mixed and Augmented Reality (ISMAR), 2011 IEEE pp. 121—126 DOI 10.1109/ISMAR.2011.6092377, 978-1-4577-2183-0
[RC11] 3D is here: point cloud library (PCL) 2011 IEEE International Conference on Robotics and Automation (ICRA), 2011 IEEE pp. 1—4 DOI 10.1109/ICRA.2011.5980567 978-1-61284-386-5
[SX14] Sliding Shapes for 3D Object Detection in Depth Images Computer Vision - ECCV 2014: 13th European Conference, Zurich, Switzerland, September 6-12, 2014, Proceedings, (David Fleet Tomas Pajdla Bernt Schiele Tinne Tuytelaars eds.), 2014 Springer , pp. 634—651 DOI 10.1007/978-3-319-10599-4_41, 978-3-319-10598-7
[TAC11] Direct iterative closest point for real-time visual odometry 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops), 2011 IEEE pp. 2050—2056 DOI 10.1109/ICCVW.2011.6130500, 978-1-4673-0062-9
[vKP10] Survey of augmented reality technologies, applications and limitations The International Journal of Virtual Reality, 2010 2 1—20 1081-1451
[VLF04] Combining edge and texture information for real-time accurate 3D camera tracking Third IEEE and ACM International Symposium on Mixed and Augmented Reality ISMAR 2004, 2004 IEEE pp. 48—56 DOI 10.1109/ISMAR.2004.2, 0-7695-2191-6
[WVS05] Adaptive line tracking with multiple hypotheses for augmented reality Fourth IEEE and ACM International Symposium on Mixed and Augmented Reality (ISMAR'05), 2005 IEEE pp. 62—69 DOI 10.1109/ISMAR.2005.8 0-7695-2459-1
[WWS07] Adaptable model-based tracking using analysis-by-synthesis techniques Computer Analysis of Images and Patterns: 12th International Conference, CAIP 2007, Vienna, Austria, August 27-29, 2007. Proceedings, (Walter G. Kropatsch Martin Kampel Allan Hanbury eds.), 2007 Springer Berlin pp. 20—27 DOI 10.1007/978-3-540-74272-2_3 978-3-540-74271-5
[ZDB08] Trends in augmented reality tracking, interaction and display: a review of ten years of ISMAR ISMAR '08 Proceedings of the 7th IEEE/ACM International Symposium on Mixed and Augmented Reality, (Mark A. Livingston ed.), 2008 IEEE pp. 193—202 DOI 10.1109/ISMAR.2008.4637362, 978-1-4244-2840-3
Fulltext ¶
-
 Volltext als PDF
(
Size
5.0 MB
)
Volltext als PDF
(
Size
5.0 MB
)
License ¶
Any party may pass on this Work by electronic means and make it available for download under the terms and conditions of the Digital Peer Publishing License. The text of the license may be accessed and retrieved at http://www.dipp.nrw.de/lizenzen/dppl/dppl/DPPL_v2_en_06-2004.html.
Recommended citation ¶
Otto Korkalo, and Svenja Kahn, Real-time depth camera tracking with CAD models and ICP. Journal of Virtual Reality and Broadcasting, 13(2016), no. 1. (urn:nbn:de:0009-6-44132)
Please provide the exact URL and date of your last visit when citing this article.

