GRAPP 2007
A Physically Based Transmission Model of Rough Surfaces
First presented at the International Conference on Computer Graphics Theory and Applications (GRAPP) 2007,
extended and revised for JVRB
urn:nbn:de:0009-6-14988
Abstract
Transparent and translucent objects involve both light reflection and transmission at surfaces. This paper presents a physically based transmission model of rough surface. The surface is assumed to be locally smooth, and statistical techniques is applied to calculate light transmission through a local illumination area. We have obtained an analytical expression for single scattering. The analytical model has been compared to our Monte Carlo simulations as well as to the previous simulations, and good agreements have been achieved. The presented model has potential applications for realistic rendering of transparent and translucent objects.
Keywords: Transmission Model, BTDF, Rough Surface, Monte Carlo Simulation, Light Scattering
Subjects: Monte-Carlo-Simulation, Light Scattering, Image Synthesis, Distribution Function
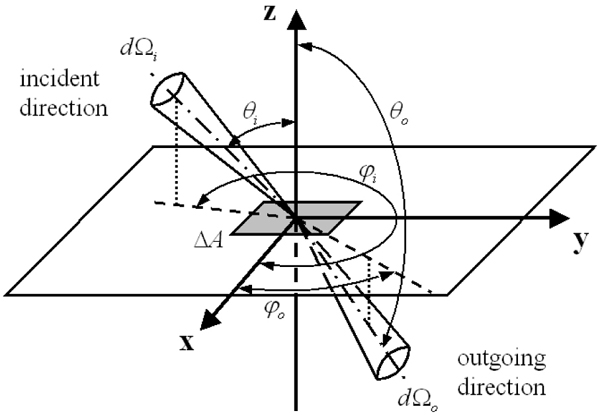
Light scattering by objects is generally characterized by a bidirectional scattering distribution function (BSDF) [ Gla95 ].
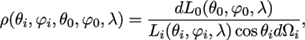 (1)
(1)
which is the ratio of the scattered radiance dL0 in the outgoing direction (θ0, φ0) to the irradiance Licos θidΩi in the direction (θi, φi) (Figure 1) at wavelength λ. When referring to reflection or transmission, a BSDF becomes a bidirectional reflectance distribution function (BRDF) or a bidirectional transmittance distribution function (BTDF). This paper studies the case of transmission.
In computer graphics applications, materials may be classified into three major types: opaque, transparent and translucent. An opaque object only involves reflection, a transparent object involves both reflection and transmission, and a translucent object has volumetric scattering in addition to reflection and transmission at the object surface. Thus, a transmission model is needed for not only transparent but also translucent objects. Such objects include glass wares, plastics, ices, biological tissues, marbles, waxes, and so on.
There has been extensive research on modelling BRDFs in computer graphics, but studies on BTDFs are limited. Different from at an opaque surface, a scattering process at a surface of some transparent or translucent material is generally a combination of reflection and transmission events, and the number of the events may be one (single scattering), two or more (multiple scattering). Solving the case of single scattering is a basis for solving the case of multiple scattering.
This paper presents a realistic transmission model of rough surfaces. We follow the same assumptions of rough surfaces as presented in the surface reflection model [ Sun07 ]. The key point of these assumptions is that the surface is sufficiently smooth locally (tangent plane approximation) and statistical techniques can be applied to calculate light transmission through a local illumination area (statistical approach efficiency). We have obtained an analytical expression for single scattering. This model has been compared to our Monte Carlo simulations as well as to the previous simulations, and good agreements have been achieved.
Existing BRDF models commonly consist of the diffuse and specular terms. The diffuse component is typically Lambertian, but the specular term differs in various models. A simple approach describes the specular component with an empirical function, such as the models of Phong [ Pho75 ], Ward [ War92 ], and Lafortune et al. [ LFTG97 ].
Deriving accurate models needs physically based approaches. One approach uses the Kirchhoff theory with the tangent plane approximation of the surface [ BS63, HTSG91 ]. Another approach is based on the microfacet assumption of Torrance and Sparrow [ TS67 ]. In this approach, the specular term is expressed as a product of the Fresnel coefficient, masking and shadowing factor, and surface orientation probability [ Bli77, CT82 ]. Ashikhmin et al. [ APS00 ] developed an analytic model to remove the limitation of V-shaped grooves needed for the traditional microfacet model. Recently, Sun [ Sun07 ] reviewed all the previous illumination models, refined the assumptions of rough surface, and derived an illumination model of rough surface by using statistical techniques.
To our best knowledge, two transmission models exist in computer graphics. The first was proposed by He [ He93 ] based on the Kirchhoff theory, and the second by Stam [ Sta01 ] as an extension from Cook-Torrance′s reflection model [ CT82 ]. In practice, the rendering of light transmission is rather simple, typically based on a formula that extends Phong′s reflection model to the case of transmission.
Beyond computer graphics, some research has been conducted to numerically simulate transmission. One example is the work of Nieto-Vesperinas et al. [ NVSGSD90 ] where light transmission at rough surfaces was computed using a Monte Carlo method.
Since transmission at a surface is a part of the problem of object translucency, we briefly review some research on translucency models. Hanrahan and Krueger [ HK93 ] developed a pioneering model of subsurface scattering using the linear transport theory. Jensen and Christensen [ JC98 ] studied light transport in participating media using Monte Carlo bi-directional ray tracing and volumetric photon mapping. Dorsey et al. [ DEJ99 ] simulated subsurface scattering of weathered stones using Monte Carlo ray tracing. Pharr and Hanrahan [ PH00 ] developed a Monte Carlo approach to solve generic scattering equations. Stam [ Sta01 ] used the radiative transfer equation to model subsurface scattering of human skins. Koenderink and van Doorn [ KvD01 ] studied subsurface scattering with a diffusion approximation of light transport theory. Jensen et al. [ JMLH01 ] proposed an analytic model of BSSRDF, and later Jensen et al. [ JB02 ] developed a two-pass technique to efficiently render translucent objects. Recently, Wang et al. [ WTL05 ] presented a technique based on pre-computed light transport to render translucent objects, and Mertens et al. [ MKB05 ] proposed an efficient algorithm to render the local effect of subsurface scattering. These studies focused on the subsurface or volumetric scattering, and light transmission at the surface was not considered.
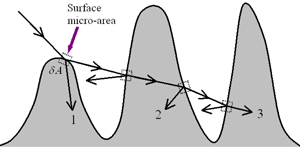
Light transmission processes at a rough surface can
be classified into single and multiple scattering. In
single scattering (ray 1 in Figure 2), a light ray
is scattered one time (this is in fact a refraction at
the local area). In multiple scattering (ray 2 or 3 in
Figure 2), there are multiple times of reflection and transmission. The total BTDF may be expressed
as
ρtotal = ρsingle + ρmultiple
(2)
where ρsingle and ρmultiple are the contributions from single and multiple scattering, respectively.
Figure 2. Light transmission processes of single scattering (ray 1) and multiple scattering (rays 2 and 3).
The assumptions and conditions of our considered surface are similar to the surface reflection model [ Sun07 ] where the focus was on reflection, but now the focus is on transmission. For convenience, the assumptions are listed below:
-
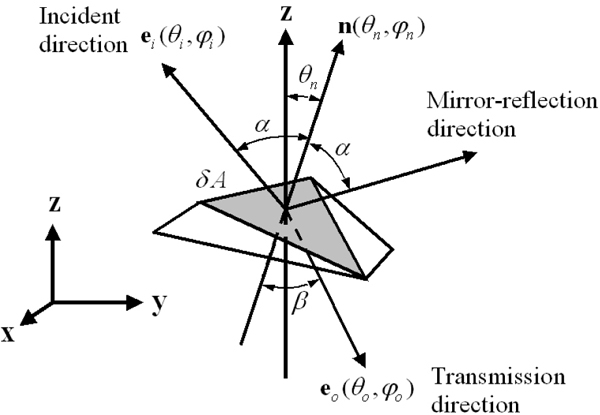
Any surface micro-area δA (see Figure 2) has size much larger than wavelength, so the light diffraction can be ignored. And also δA is sufficiently smooth such that it can be replaced with its local tangent plane (tangent plane approximation).
-
Any local illumination area ΔA for the definition of BTDF (Figure 1) contains many surface micro-areas δA. As a result, it is valid that the light transmission through ΔA can be calculated as the statistical average of light transmission through δA (statistical approach sufficiency).
-
The surface properties remain the same in ΔA. These properties include the material aspect such as the optical constants, and the geometric aspect such as the statistics of the surface profile (surface homogeneity).
-
The surface profile is a height field. That is, for any line parallel with the z-axis, the line will intersect with the surface profile exactly one time (height-field surface).
-
A combined probability can be approximated as a product of the individual probabilities (separable combined probability, see below).
-
The correlation between the incident and outgoing directions are ignored. As additional conditions, we assume that the surface is isotropic and has a Gaussian height probability density and correlation function.
For most natural surfaces, the surface height distribution can be described well with a Gaussian function [ Tho99 ]. The probability density function of surface height is
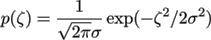 (3)
(3)
where ζ is the surface height, and σ is the standard deviation or RMS.
To describe surface roughness, we need to consider the
surface height correlation. A two-point correlation
function is generally defined as
C(r) = < h(r0)h(r0 + r) >/σ1
(4)
which involves the average of the product of heights at
points r0
and r0 + r on the z = 0 plane. Since the surface
is isotropic, we can write C(r) = C(r). We adopt the
following correlation function [
Ogi91
]
C(r) = exp(-r2/τ2) (5)
where τ is the correlation length. Now we define the
surface smoothness as
s = τ/σ (6)
The smaller is s, the rougher the surface; vice versa.
Given surface profile ζ = h(x,y) the orientation of a micro-area δA is described by the partial derivatives (ζ'x, ζ'y)
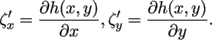 (7)
(7)
The probability for the orientation of a micro-area δA in dζ'xdζ'y is given as (in [ Sun07 ])
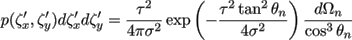 (8)
(8)
where dΩn
is differential solid angle of n(θn,φn)
dΩn = sinθndθndφn
. (9)
Given a micro-area δA (Figure 3), the incident radiance
Li(θi, φi) and the transmitted radiance L0(θ0, φ0) are
related as,
L0(θ0, φ0)cosβdΩ0 = Ft(α,λ)Li(θi,φi)δ(n,ei,e0)cosαdΩi
(10)
where β is the transmission angle for the incident angle
α, dΩ0
is the solid angle in the transmission direction, dΩi
is the solid angle in the incident direction, and Ft(α, λ) is
the Fresnel coefficient of transmission averaged over
polarizations at the wavelength λ. δ(n,ei,e0) is a Dirac
delta function. That is, when n,ei
, ande0
are coplanar
and sinα = n sinβ (n is the relative index of refraction),
δ(n,ei,e0) = 1; otherwise δ(n,ei,e0) = 0. The radiant
flux δΦ(θ0,φ0) through a micro-area δA is given
as
δΦ(θ0,φ0) = L0(θ0,φ0)cosβδAdΩ0 = Ft(α, λ)(θi,φi)δ(n,ei,e0)cosαδAdΩi
(11)
Since a local illumination area ΔA over which the
BTDF is defined (Figure 1) contains many micro-areas
δA, the total radiant flux overΔA contains contributions
from all possible micro-areas,
ΔΦ(θ0,φ,0) = ∑ΔAV(δA)δΦ(θ0,φ0) = Li(θi,φi)cosαdΩi∑ΔAV(δA)Ft(α, λ)δ(n,ei,e0)δA (12)
where V(δA) is a visibility function describing the probability of a micro-area δA that is visible in both directions ei(θi,φi) and e0(θ0,φ0). The radiance to the transmission direction e0(θ0,φ0) is given as
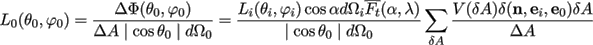 (13)
(13)
Because θ0 is measured from the positive z-axis (see Figure 1) and its value is within [π / 2, π], we take its absolute value in the above equation. Substituting Eq. 13 into Eq. 1, we obtain
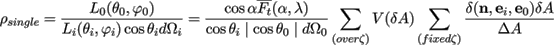 (14)
(14)
Here the summation over the local illumination area
ΔA has been decomposed into the summation over all
micro-areas at a fixed height ζ and the summation over all
micro-areas at different heights. Since the visibility
function V(δA) at a fixed height remains the same for
given incident and outgoing directions, it has been
put outside the inner summation for a fixed height.
Considering that the projected area of δA on the z = 0
plane is
(δA)⊥ = δAcosθn (15)
where θn is the polar angle of the normal n(θn, φn) of δA (see Figure 3), the portion of the total projected areas ∑fixed ζ(δA)⊥)δ(n,ei,e0) in ΔA is the probability of a surface point with height in differential interval [ζ,ζ+dζ] and with orientation in intervals [ζ'x,ζ'x+dζ'x] and [ζ'y,ζ'y+dζ'y]. Thus
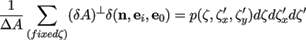 (16)
(16)
From Assumption 5, the combined probability density
function can be decomposed as
p(ζ,ζ'x,ζ'y) = p(ζ)p(ζ'x,ζ'y). (17)
Applying Eqs. 16, 17 into Eq. 14, we obtain
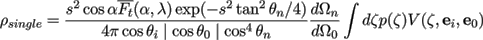 (18)
(18)
This equation may be further expressed as
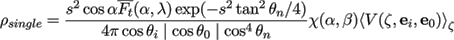 (19)
(19)
where the function χ(α,β) describes dΩn/dΩ0 (see Appendix A), and
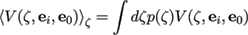 (20)
(20)
is the averaged bistatic visibility function. A bistatic
visibility function simultaneously involves the incident
direction ei
and the outgoing direction e0
. For light
transmission, since ei
points into the original medium and
e0
into the new medium, the correlation between the two
directions can be ignored, as stated in Assumption 6.
Therefore
V(ζ, ei,e0) ≈ V(zeta, θi)V(ζ, θ0), (21)
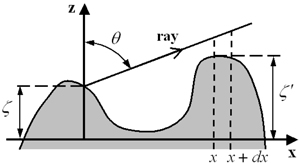
where V(ζ, θ) is an individual visibility function that describes the probability of being visible for a ray starting at height ζ and with angle θ (Figure 4), and accordingly,
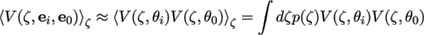 (22)
(22)
We further approximate Eq. ( 22) as
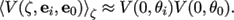 (23)
(23)
where V(0,θi) and V(0,θ0) are the individual visibility functions for the incident and outgoing directions when the ray starts from ζ = 0. From the previous study [ Sun07 ],
 (24)
(24)
where k0 = 0.7. Thus, we finally obtain
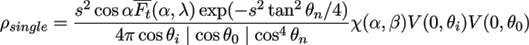 (25)
(25)
where χ(α, β) is given in the Appendix.
Figure 5. BTDF for different n and s. Parameters are θi = 30°, n = 1/1.4 for the first row, and n = 1.4 for the second row. From the left to right, the values of s are 6, 3, and 1, respectively.
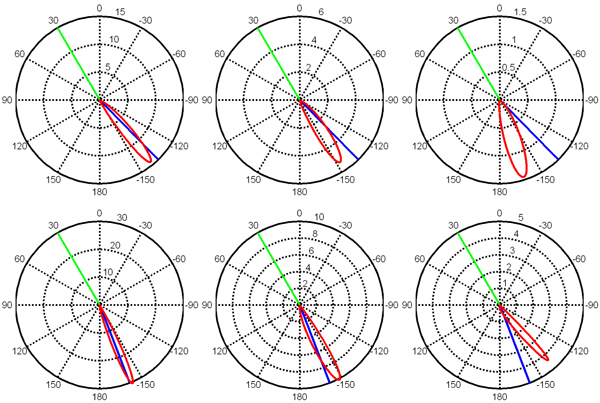
Figure 5 shows ρsingle for different values of relative index of refraction (IOR) n and smoothness s. The solid straight lines (in green) in the upper hemisphere indicate the incident direction, and the solid straight lines (in blue) in the lower hemisphere indicate the transmission direction. ρsingle has a sharp lobe and shows the off-specular effect. When n < 1 (the first row), as the outgoing direction changes from θ = -90° to θ = 180°, ρsingle increases gradually and reaches a maximum, then decreases rapidly. Also, the direction that ρsingle has the maximum shifts toward θ = 180° with the decrease of s. In contrast, for n > 1 (the second row), when the outgoing direction changes from θ = -90° to θ = 180°, ρsingle increases rapidly and reaches the maximum, then decreases gradually. Moreover, the direction for the maximum ρsingle shifts towardθ = -90° with the decrease of s.
The plots in Figure 5 can be explained as below. First, when the surface is smooth, most micro-areas distribute around θn = 0° and they contribute to ρsingle with α → θi . Second, Fresnel's transmission coefficient has the maximum for incident angle α = 0°, and decreases with the increase of α. Therefore, those micro-areas with orientation around the incident direction have large Fresnel's transmission coefficients. These two factors compete with each other. And also, for n < 1, the refraction angle β is larger than the incident angle α, and vice versa. These result in the plot shapes in Figure 5. With the decrease of s, the maximum distribution of orientations of micro-areas tends to shift from θn = 0° toward θn = 90°, which results in a shift of the direction for the maximum ρsingle .
Figure 6. BTDF for different n and s. Here θi = 0°, and other parameters and notations are the same as Figure 5
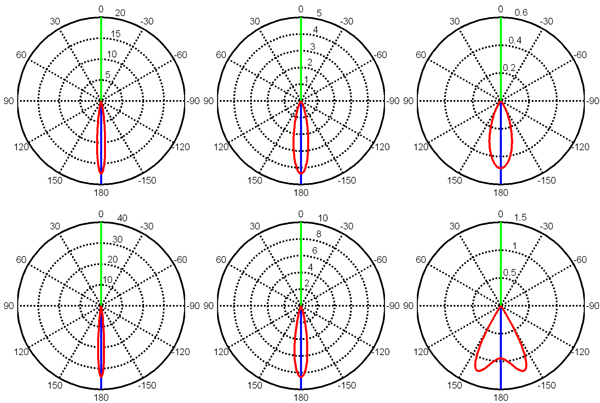
For the normal incidence, ρsingle for different values of n and s is shown in Figure 6. For n < 1, the sharp lobe becomes wider with the decrease of s, same as Figure 5. However, for the cases n > 1 in both Figures 5 and 6, although the sharp lobes for s = 3 are all wider than those for s = 6, the sharp lobes for s = 1 have different shapes. Consider the rotational geometry, ρsingle for s = 1 in Figure 6 is actually a lobe with an indented peak. We can understand this by the micro-area model. For rough surfaces (s = 1), most micro-areas distribute with orientations θn ≫ 0°, and therefore the transmitted light by single scattering tends to travel along the direction with 90° ≪ θ0 ≪ 180°. This results in the indentation of the lobe in Figure 6. However, the probability of ray blocking is higher for the rays propagating along this direction. This results in the sharper shape for s = 1 in Figure 5.
In our Monte Carlo simulation, given a Gaussian rough surface with its mean equal to zero and standard deviation σ, totally N light rays are shot from the incident direction ei , each ray carrying a weight Wl(l=1,2,...,N) that represents its radiance flux intensity. Once a shot ray hits the surface profile, it typically splits into a reflected and a transmitted ray. When the total internal reflection occurs, only a reflected ray is generated.
The surface height at which a shot ray intercepts with the profile is determined by the probability density function of surface height and a generated random number (all the generated random numbers in this paper are uniformly distributed between 0 and 1). The normal direction of this intersection point is obtained by the orientation probability density function with two generated random numbers.
We set the incident flux density to 1. Then the weight of
the lth shot ray is given as
Wl = V(ζ1, θi)cosα/cosθn (26)
where ζ1 is the surface height that the shot ray first intercepts with, α is the incident angle in the local area, and cosθn is involved because Eq. 16 just describes the probability distribution of δA⊥ at a fixed height.
When a ray with weight W hits the surface profile, it splits into a reflected and transmitted ray, and the weight of the reflected ray is Fr(α, λ)W and that of the transmitted ray is Ft(α, λ)W. Therefore, after each ray splitting, the generated rays will decrease in intensities. Once the weight of a newly generated ray is lower than the threshold, the tracking process terminates. Otherwise, it will be tracked continuously; whether it is blocked or not depends on its propagation direction, visibility function, and a generated random number.
The radiance to the transmission direction e0(θ0,φ0) is obtained as
 (27)
(27)
where ΔΩ0 is the solid angle along e0(θ0,φ0), and ∑l ∈ ΔΩ0 Wl calculates the sum of the weights of those rays transmitted into ΔΩ0 . Consider that the incident irradiance is cosθi (since incident flux density is set to 1), the BTDF can be calculated by
 (28)
(28)
In discussion below we may replace ρ with ρ ∣ cosθ0 ∣ based on two considerations. First, the previous simulations by Nieto-Vesperinas et al. [ NVSGSD90 ] calculated the transmitted light intensity, which is proportional to ρ ∣ cosθ0 ∣. For convenience of comparing the results, we need to use ρ ∣ cosθ0 ∣ instead of ρ. Second, Eq. ( 28) contains 1/ ∣ cosθ0 ∣ and ∑l ∈ ΔΩ0 Wl . When θ0 → π, ∣ cosθ0 ∣ → 0. However, we cannot take ΔΩ0 → 0 for the calculation of Eq. (28). Therefore, ρ might diverge at θ0 → 90°.
Figure 7 compares our analytical model and simulations. Nieto-Vesperinas et al. [ NVSGSD90 ] considered perpendicular and parallel polarizations separately. For comparison, we calculate the average of the two polarizations. In our analytical model and simulation, light intensity can be calculated by ρ ∣ cosθ0 ∣ ΔA. Since we do not know the value of ΔA used for the simulation of Nieto-Vesperinas et al., we find it by matching our analytical model with their results for θi = 0°. In Figure 7, the comparison shows a very good match.
Figure 7. Comparison between our analytical model and simulations. The curves with x marks are from the analytical model, the dot curves from the simulations of Nieto-Vesperinas et al. [ NVSGSD90 ], and the solid curves from our simulations. Here, n = 1.411, s = 2.522, (a) θ i = 0°, (b) θ i = 20°, (c) θ i = 40°, and (d) θ i = 60°.
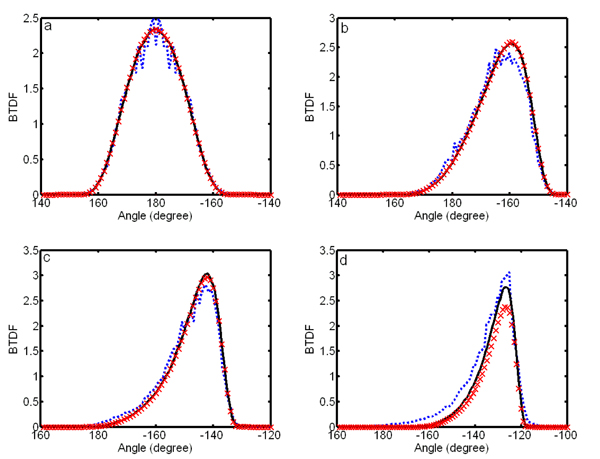
Figure 8. Comparison between simulation and analytical model. The solid curves are from our simulation, and the curves with x marks from analytical model. Here, θ i = 30°, n = 1/1.4, (a) s = 6, (b) s = 3, (c) s = 1, and (d) s = 0.5.
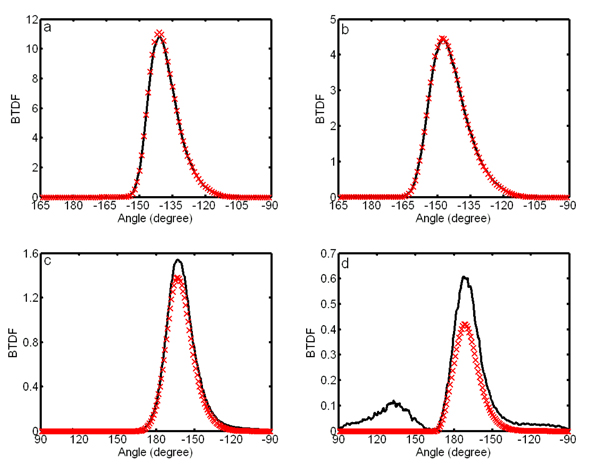
Figure 9. Comparison between simulation and analytical model. The solid curves are from our simulation, and the curves with x marks from analytical model. Here, θ i = 30°, n = 1.4, (a) s = 6, (b) s = 3, (c) s = 1, and (d) s = 0.5.
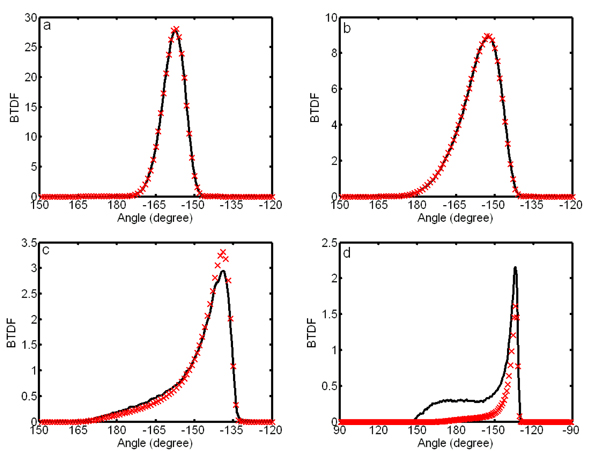
Figures 8 and 9 compare our simulation and the analytical model for different values of n and s. For smooth and moderately smooth surfaces (s is 3 or 6), the analytical model agrees well with the simulation. With small s, the difference between the model and simulation increases. This is because our analytical model only considers single scattering. For smooth surfaces, light transmission is dominated by single scattering. Overall, the model has a good match with the simulation. For rough surfaces (s is small), multiple scattering plays an important role and should be considered.
We have implemented this analytical model for image rendering. In each image, we have linearly scaled the color components so that the maximum value of all color components is 255.
Figure 10 shows the rendered transparent object with semi-infinite depth for different n and s. The face of this transparent object is a rough, plate surface. The distance from the eye to the center of the face is 0.8 times width of the face. A far point light source is set inside the object medium. Therefore, the incident light is almost perpendicular to the medium surface. Figure 11 shows the rendered images of the same transparent object with the same parameters and notations as Figure 11 , except the point light source is closer to the face.
Figures 12 and 13 show rendered sculptures for different s. In each image, a far point light source is set in the back. The distance from the eye to the sculpture is about 0.75 times the size of the sculpture. The index of refraction of the sculptures is 1.4. In Figure 13 , the foreheads in the images for s = 4 and s = 5 do not look smooth, and this is due to the fact that the mesh of this sculpture is not dense.
Figure 10. Rendered transparent objects with semi-infinite depths for different n and s. Here the parameters and notations are the same as Figure 5.

Figure 11. Rendered transparent objects with semi-infinite depths for different n and s. A near point light source is set inside the object medium (the distance from the point light source to the face is 0.8 times width of the face). Other parameters and notations are the same as Figure 10.

Figure 12. Rendered images of Atenea for different s. From the left to the right, the values of s are 2, 3, 4, and 5, respectively.

Figure 13. Rendered images of Angel for different s. The values of s are taken as same as Figure 12.

This paper presents a physically based transmission model of rough surface. We have obtained an analytical expression for single scattering. The analytical expression has been compared to our Monte Carlo simulations as well as to the previous simulations, and good agreements have been achieved. This model has been used for image rendering.
In future work, the model can be applied to render realistic transmission effects. And also, it could be taken into consideration to study object translucency. To further verify this model, we may generate 2D surfaces for given surface height standard deviation and correlation length, and compute the average of transmission through the surfaces. The current analytical model has not considered multiple scattering, and both the analytical model and simulation have not considered polarization effects. We will consider them in our further work.
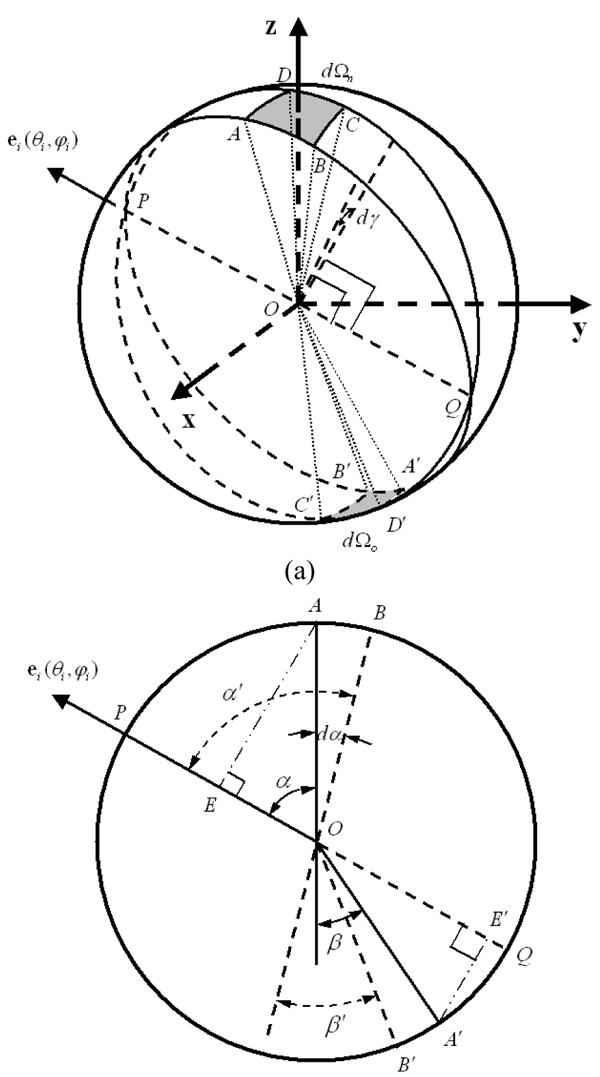
Here we derive the relationship between the differential solid angles dΩ0
and dΩn
. Given an unit sphere (Figure 14), the area ABCD corresponds to dΩn
and the area A'B'C'D' to dΩ0
. The points A, B, A', and B' are coplanar, and similarly the points C, D, C' and D'. The planes ABA'B' and DCD'C' intersects at the line POQ, and the angle between them is dγ. Therefore, the length of the curve segment AD is
| AD | = | AE | ⋅ dγ = sinα ⋅ dγ. (A1)
Since | AB | = dα, so we obtain
dΩ = | AD | ⋅ | AB | = sinα ⋅ dγdα (A2)
The Snell's law gives the following relations:
sinα = n⋅sinβ (A3)
and
sin α' = sin(α + dα) = n⋅sinβ' = n⋅sin(β + dβ) (A4)
where n is the relative index of refraction n > 1 and dβ is defined as
dβ = β' - β (A5)
From Eq. A4 we can obtain
sinα ⋅ cos(dα) + cosα ⋅ sin(dα) = n ⋅ [sinβ ⋅ cos(dβ) + cosβ ⋅ sin(dβ)] (A6)
We make the following approximations:
cos(dα) ≈ 1, sin(dα) ≈ dα,
cos(dβ) ≈ 1, sin(dβ) ≈ dβ. (A7)
Substituting Eqs. (A3) and (A7) into Eq. (A6), we obtain
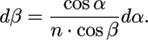 (A8)
(A8)
From Figure 14(b) we obtain
β' = β - ∠A'OB' + dα. (A9)
Therefore, we obtain
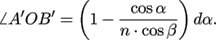 (A10)
(A10)
The length of the curve segment A'B' is
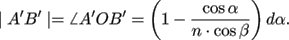 (A11)
(A11)
The length of the curve segment A'D' is
| A'D' | = | A'E' | ⋅ dγ = sin(∠A'OQ)dγ = sin(α - β)dγ (A12)
Therefore, we obtain
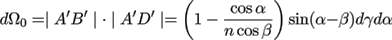 (A13)
(A13)
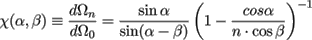 (A14)
(A14)
Although Eq.(A14) is derived for n > 1, it is easy to prove that this expression also holds for n < 1.
[APS00] A microfacet-based BRDF generator, Proceedings of the 27th annual conference on Computer graphics and interactive techniques, 2000, pp. 65—74, isbn 1-58113-208-5.
[Bli77] Models of light reflection for computer synthesized picture, Proceedings of the 4th annual conference on Computer graphics and interactive techniques, 1977, pp. 192—198, issn 0097-8930.
[BS63] The Scattering of Electromagnetic Waves from Rough Surfaces, 1963, Macmillan, New York, isbn 0080100074.
[CT82] A Reflectance Model for Computer Graphics, ACM Transactions on Graphics (1982), no. 1, 7—24, issn 0730-0301.
[DEJL99] Modeling and rendering of weathered stone, Proceedings of the 26th annual conference on Computer graphics and interactive techniques, 1999, pp. 225—234, isbn 0-201-48560-5.
[FC85] Numerical simulation of scattering from simple and composite random surfaces, 1995, Journal of the Optical Society of America. A, Optics and image science, 2(1985), no. 12, 2274—2284, issn 0740-3224.
[Gla95] Principles of Digital Image Synthesis, 1995, Morgan Kaufmann Publishers, San Francisco, CA, isbn 1558602763.
[He93] Physically-based models for the reflection, transmission and subsurface scattering of light by smooth and rough surfaces, with applications to realistic image synthesis, Cornell University, Ithaca, New York, 1993.
[HK93] Reflection from layered surface due to subsurface scattering, Proceedings of the 20th annual conference on Computer graphics and interactive techniques, 1993, pp. 165—174, isbn 0-89791-601-8.
[HTSG91] A comprehensive physical model for light reflection, Proceedings of the 18th annual conference on Computer graphics and interactive techniques, 1991, pp. 175—186, isbn 0-201-56291-X.
[JB02] A rapid hierarchical rendering technique for translucent materials, ACM Transactions on Graphics, (2002), no. 3, 576—581, issn 0730-0301.
[JC98] Efficient Simulation of Light Transport in Scenes with Participating Media Using Photon Maps, Proceedings of the 25th annual conference on Computer graphics and interactive techniques, 1998, pp. 311—320, isbn 0-89791-999-8.
[JMLH01] A practical model for subsurface light transport, Proceedings of the 28th annual conference on Computer graphics and interactive techniques, 2001, pp. 511—518, isbn 1-58113-292-1.
[KvD01] Shading in the case of translucent objects, Proc. SPIE, Volume 4299, 2001, pp. 312—320, isbn 0-8194-3977-0.
[KM31] Numerical simulation of scattering from simple and composite random surfaces, Zeitschrift Für Technische Physik, (1931), 593—620, issn 0373-0093.
[LFTG97] Non-linear approximation of reflectance functions, Proceedings of the 24th annual conference on Computer graphics and interactive techniques, 1997, pp. 117—126, isbn 0-89791-896-7.
[MKBR05] Efficient rendering of local subsurface scattering, Computer Graphics Forum, (2005), no. 1, 41—49, issn 0167-7055.
[NVSGSD90] Light transmission from a randomly rough dielectric diffuser: theoretical and experimental results, Opt. Lett., (1990), no. 22, 1261—1263, issn 0146-9592.
[Ogi91] Theory of Wave Scattering from Random Rough Surfaces, 1991, Adam Hilger, Bristol, isbn 0750300639.
[PH00] Monte carlo evaluation of non-linear scattering equations for subsurface reflection, Proceedings of the 27th annual conference on Computer graphics and interactive techniques, 2000, pp. 75—84, isbn 1-58113-208-5.
[Pho75] Illumination for computer generated images, Communications of ACM, (1975), no. 6, 311—317, issn 0001-0782.
[Sta01] An illumination model for a skin layer bounded by rough surfaces, Proceedings the 21th Eurographics Workshop on Rendering Techniques, 2001, Springer, Steven J. Gortler and Karol Myzskowski (Eds.), pp. 39—52, isbn 3-211-83709-4.
[Sun07] Statistical ray method for deriving reflection models of rough surfaces, J. Opt. Soc. Am. A, (2007), no. 3, 724—744, issn 1084-7529.
[Tho99] Rough Surfaces, 1999, 2nd Edition, Imperial College Press, London, isbn 1860941001.
[TS67] Theory for off-specular reflection from roughened surfaces, Journal of the Optical Society of America, (1967), no. 9, 1105—1114, issn 0740-3224.
[War92] Measuring and modeling anisotropic reflection, Proceedings of the 19th annual conference on Computer graphics and interactive techniques, 1992, pp. 265—272, isbn 0-89791-479-1.
[WTL05] All-Frequency Interactive Relighting of Translucent Objects with Single and Multiple Scattering, ACM Transactions on Graphics (TOG), (2005), no. 3, 1202—1207, issn 0730-0301.
Volltext ¶
-
 Volltext als PDF
(
Größe:
4.1 MB
)
Volltext als PDF
(
Größe:
4.1 MB
)
Lizenz ¶
Jedermann darf dieses Werk unter den Bedingungen der Digital Peer Publishing Lizenz elektronisch übermitteln und zum Download bereitstellen. Der Lizenztext ist im Internet unter der Adresse http://www.dipp.nrw.de/lizenzen/dppl/dppl/DPPL_v2_de_06-2004.html abrufbar.
Empfohlene Zitierweise ¶
Huiying Xu, and Yinlong Sun, A Physically Based Transmission Model of Rough Surfaces. JVRB - Journal of Virtual Reality and Broadcasting, 5(2008), no. 9. (urn:nbn:de:0009-6-14988)
Bitte geben Sie beim Zitieren dieses Artikels die exakte URL und das Datum Ihres letzten Besuchs bei dieser Online-Adresse an.