GRAPP 2007
The art to keep in touch: The 'good use' of Lagrange multipliers
First presented at the First International Conference
on Computer Graphics Theory and Applications
(GRAPP 2007),
extended and revised for JVRB
urn:nbn:de:0009-6-12767
Abstract
Physically-based modeling for computer animation allows to produce more realistic motions in less time without requiring the expertise of skilled animators. But, a computer animation is not only a numerical simulation based on classical mechanics since it follows a precise story-line. One common way to define aims in an animation is to add geometric constraints. There are several methods to manage these constraints within a physically-based framework. In this paper, we present an algorithm for constraints handling based on Lagrange multipliers. After few remarks on the equations of motion that we use, we present a first algorithm proposed by Platt. We show with a simple example that this method is not reliable. Our contribution consists in improving this algorithm to provide an efficient and robust method to handle simultaneous active constraints.
Keywords: Physically-based animation, constraints, contact simulation
Subjects: Computer Animation, Computer Simulation
For about two decades, the computer graphics community has investigated the field of physics in order to produce more and more realistic computer animations. In fact, physically-based modeling in animation allows to generate stunning visual effects that would be extremely complex to reproduce manually. On one hand, the addition of physical properties to 3D objects automates the generation of motion just by specifying initial external forces. On the other hand, physically-based animations are even more realistic than traditional key-framed animations that require the expertise of many skilled animators. As a consequence, the introduction of physically-based methods in modeling and animation significantly reduced the cost and production time of computer generated movies. But, one main drawback of this kind of framework is that it relies on heavy mathematics usually hard to tackle for a computer scientist. A second main disadvantage concerns the input of a physically-based animation: in fact, forces and torques are not really user-friendly since it is really difficult to anticipate a complex motion just by specifying an initial set of external forces.
A computer animation is definitely not a numerical simulation because it follows a story-line. According to Demetri Terzopoulos [ TPB89 ], an animation is simulation plus control. One way to ensure that the objects fulfill the goals defined by the animator is to use geometric constraints. A constraint is an equality or an inequality that gathers different parameters of the animation like the total time elapsed, the positions or the orientations of the moving objects. In a less general way, mechanical simulations also benefit from the use of constraints in order to prevent interpenetration between physical objects for example.
There are several methods to handle constraints, summarized in a survey paper by Baraff [ Bar93 ]. But, since our research work is mostly devoted to mechanical simulation, we decided to focus on the use of Lagrange multipliers to manage geometric constraints. In fact, numerical simulations require robust and reliable techniques to ensure that the constraints are never violated. Moreover, with this method we are also able to measure the amount of strain that is necessary to fulfill a given constraint. In this paper, we present a novel algorithm to manage efficiently several simultaneous active geometric constraints. We begin by detailing the physical equations that we use before presenting Platt′s algorithm [ Pla92 ] that is the only algorithm of this type based on Lagrange multipliers. With a simple example, we demonstrate that this algorithm is not suitable for handling simultaneous active constraints. We then introduce our own contribution in order to show how to improve Platt′s algorithm to make it reliable, robust and efficient.
Lagragian dynamics consist in an extension of newtonian dynamics allowing to generate a wide range of animations in a more efficient way. In fact, Lagrange equations of motion rely on a set of unknowns, denoted as a state vector x of generalized coordinates, that identifies the real degrees of freedom (DOF) of the mechanical systems involved. Within this formalism, the DOF are not only restricted to rotations or translations. For example, a parameter u ∈ [0,1] which gives the relative position of a point along a 3D parametric curve can be considered as a single generalized coordinate.
The evolution of a free mechanical system only subject to a set of external forces is ruled by the Lagrange equations of motion ( 1 ).
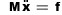 (1)
(1)
M is the mass matrix.
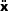 is the second time derivative of
the state vector. Finally, the vector f corresponds to the
sum of external forces. For more details concerning this
formalism, we suggest to read [
Gol80
] and [
Arn89
].
is the second time derivative of
the state vector. Finally, the vector f corresponds to the
sum of external forces. For more details concerning this
formalism, we suggest to read [
Gol80
] and [
Arn89
].
By convention, an equality constraint will always be
defined as in equation ( 2 ) where
 is the set of indices of
all the equality constraints.
is the set of indices of
all the equality constraints.
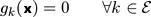 (2)
(2)
Constraints restrict the set of reachable configurations
to a subspace of
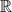 n
where n is the total number of degrees
of freedom. As mentioned before, there exists three
main methods to integrate constraints in equation (
1 ).
The projection method consists in modifying the
state vector x and its first time derivative
n
where n is the total number of degrees
of freedom. As mentioned before, there exists three
main methods to integrate constraints in equation (
1 ).
The projection method consists in modifying the
state vector x and its first time derivative
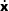 in
order to fulfill the constraint. This modification
can be performed with an iterative method like
the Newton-Raphson method [
VF02
]. Even if
this method is very simple and seems to ensure
an instantaneous constraint fulfillment, it is not
robust enough: indeed it can not guarantee that
the process converges in the case of simultaneous active constraints.
The penalty method adds new external
forces, acting like virtual springs, in order to
minimize the square of the constraint equation,
considered as a positive energy function. The
main advantage of this method is its compatibility
with any dynamic engine since it only relies
on forces. But this method leads to inexact
constraint fulfillment, allowing interpenetration
between the physical objects. In order to diminish
this interpenetration, the stiffness of the virtual
springs must be significantly increased, making
the numerical system unstable.
The Lagrange method consists in calculating the
exact amount of strain, denoted as the Lagrange
multiplier, needed to fulfill the constraint. This
method guarantees that constraints are always
exactly fulfilled. Since the use of Lagrange
multipliers introduces a set of new unknowns,
equation ( 1 ) must be completed by a set of
new equations, increasing the size of the initial
linear system to solve. But we consider that this
method is most suitable for efficiently managing
geometric constraints.
in
order to fulfill the constraint. This modification
can be performed with an iterative method like
the Newton-Raphson method [
VF02
]. Even if
this method is very simple and seems to ensure
an instantaneous constraint fulfillment, it is not
robust enough: indeed it can not guarantee that
the process converges in the case of simultaneous active constraints.
The penalty method adds new external
forces, acting like virtual springs, in order to
minimize the square of the constraint equation,
considered as a positive energy function. The
main advantage of this method is its compatibility
with any dynamic engine since it only relies
on forces. But this method leads to inexact
constraint fulfillment, allowing interpenetration
between the physical objects. In order to diminish
this interpenetration, the stiffness of the virtual
springs must be significantly increased, making
the numerical system unstable.
The Lagrange method consists in calculating the
exact amount of strain, denoted as the Lagrange
multiplier, needed to fulfill the constraint. This
method guarantees that constraints are always
exactly fulfilled. Since the use of Lagrange
multipliers introduces a set of new unknowns,
equation ( 1 ) must be completed by a set of
new equations, increasing the size of the initial
linear system to solve. But we consider that this
method is most suitable for efficiently managing
geometric constraints.
For all the reasons mentioned above, we chose the Lagrange method to manage our geometric constraints. According to the principle of virtual work, each constraint gk adds a new force perpendicular to the tangent space of the surface gk(x) = 0. The Lagrange multiplier λk corresponds to the intensity of the force related to the constraint gk . With these new forces, equation ( 1 ) is modified as follows:
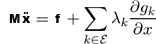 (3)
(3)
We add new equations to our system by calculating the second time derivative of equation ( 2 ), leading to equation ( 4 ).
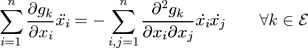 (4)
(4)
In order to correct the numerical deviation due to round-off errors, Baumgarte proposed in [ Bau72 ] a constraint stabilization scheme illustrated by equation ( 5 ). The parameter τ-1 can be seen as the speed of constraint fulfillment.
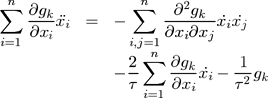 (5)
(5)
When we mix equations ( 1 ) and ( 5 ), we obtain a linear system where the second time derivative of the state vector x and the vector of Lagrange multipliers Λ are the unknowns.
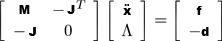 (6)
(6)
J is the jacobian matrix of all the geometric constraints and d corresponds to the right term of equation ( 5 ).
By convention, an inequality constraint will always be
defined as in equation ( 7 ) where
 is the set of indices
of all the inequality constraints.
is the set of indices
of all the inequality constraints.
 (7)
(7)
For a given state vector x, we recall the following definitions:
-
the constraint is said to be violated by x when gk(x) < 0 . This means that the state vector x corresponds to a non allowed configuration.
-
the constraint is said to be satisfied by x when gk(x) ≥ 0.
-
the constraint is said to be active when gk(x) = 0. In this case, the state vector x belongs to the boundary of the subspace defined by the inequality constraint gk .
The management of inequality constraints is more difficult than the management of equality constraints. An inequality constraint must be handled only if it is violated or active. In fact, the algorithm is a little more complicated as we explain in the next sections.
That is why we define two subsets within
 :
:
 + is the
set of indices of all handled inequality constraints and
+ is the
set of indices of all handled inequality constraints and
 -
is the set of indices of ignored inequality constraints.
Finally, we have
-
is the set of indices of ignored inequality constraints.
Finally, we have
 =
=
 - ∪
- ∪
 +. The jacobian matrix of
constraints J of equation ( 6 ) is built from all the
constraints gk
where k ∈
+. The jacobian matrix of
constraints J of equation ( 6 ) is built from all the
constraints gk
where k ∈
 ∪
∪
 +.
+.
Within the computer graphics community, the main
published method devoted to inequality constraints
management using Lagrange multipliers, known as
“Generalized Dynamic Constraints”, was proposed by
Platt in [
Pla92
]. In his paper, he describes how to use
Lagrange multipliers to assemble and simulate collisions
between numerical models. This method is an extension of
the work of Barzel and Barr [
BB88
] that specifies
how constraints must be satisfied. Moreover, Platt
proposes a method to update
 + (the set of handled
inequality constraints) during the animation. This
algorithm can be compared to classical active set methods
[
Bjo96, NW00
].
+ (the set of handled
inequality constraints) during the animation. This
algorithm can be compared to classical active set methods
[
Bjo96, NW00
].
We do not focus on collision detection that is a problem by itself. We are aware that this difficult problem can be solved in many ways, we encourage the reader to refer to the survey paper by Teschner et al. [ TKZ05 ]. During the collision detection stage, we assume that the dynamic engine may rewind time until the first constraint activation is detected. This assumption can produce an important computational overhead that can restrict our method to off-line animations production depending on the complexity of the scene simulated. In any case, this stage ensures that constraints are never violated. But, it is possible that several constraints are activated simultaneously. The main topic of this paper is to provide a reliable algorithm to handle these multiple active constraints in an efficient way.
At the beginning of the animation, Platt populates the
set  + with all the active constraints.
+ with all the active constraints.
|
Algorithm 1: Platt's algorithm |

|
For each time step, according to algorithm 1,
we solve equation ( 6 ) and update the state vector
in order to retrieve new positions and velocities at
the end of the current time step. We then check the
status of each inequality constraint. If a constraint gk
is
active, it is still handled until its Lagrange multiplier
is negative or null, that is to say that the Lagrange
multiplier corresponds to a force that prevents from
deactivation. According to the new values of the state
vector x, if the previously inactive constraint gk
is now
violated (gk(x) < 0), the constraint must be added to
 + in order to prevent the system to enter in such a
configuration.
+ in order to prevent the system to enter in such a
configuration.
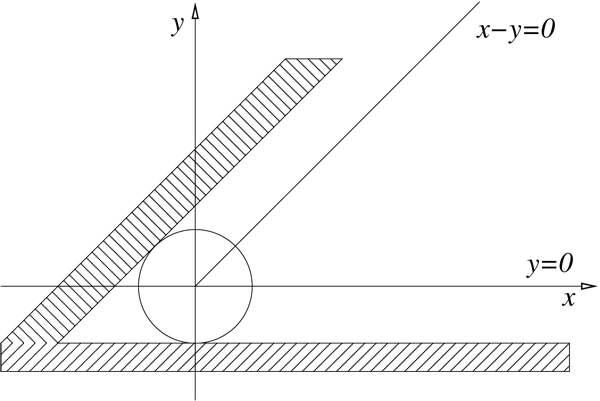
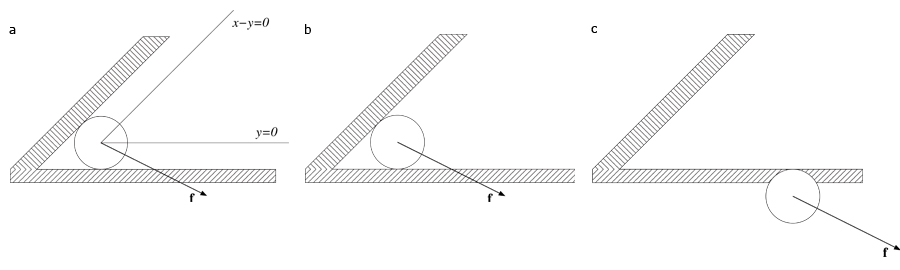
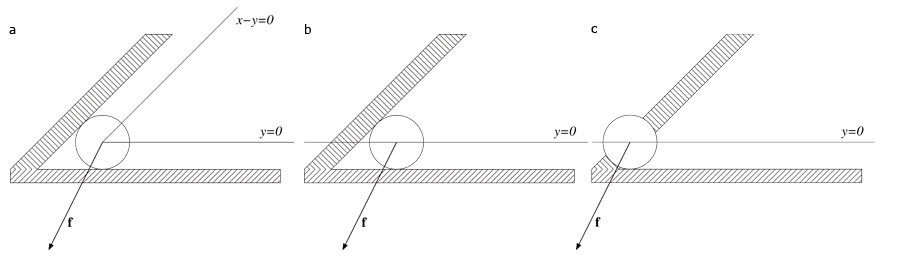
Even if this algorithm seems to give a reliable solution for inequality constraints handling, some problems remain. We set up a simple scene as in figure 1 to illustrate the insufficiencies of Platt′s method. A particle of mass m is constrained to slide on a 2D plane. It starts from an acute-angle corner modeled by two linear inequality constraints g1(x) ≥ 0 and g2(x) ≥ 0 where g1(x) = x - y and g2(x) = y. Finally, this particle is subject to a single external force f = (2,-1). In this particular case, the state vector x is composed of the 2D coordinates (x,y) of the particle. According to equation ( 1 ), the generalized mass matrix for this system is defined by:
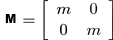 (8)
(8)
As the geometric constraints g1(x) and g2(x) are linear, their first and second time derivative do not produce any deviation term defined in equation ( 5 ):
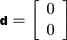 (9)
(9)
According to the initial value of the state vector
x = (0,0), the two constraints g1(x) and g2(x) are active,
so their indices are inserted in
 + and J, the jacobian
matrix of constraints, is defined as follows:
+ and J, the jacobian
matrix of constraints, is defined as follows:
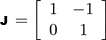 (10)
(10)
From equations ( 6 ), ( 8 ), ( 9 ), and ( 10 ), we obtain a linear system whose unknowns are the second time derivative of the state vector x and the two Lagrange multipliers λ1 and λ2 associated with g1 and g2 :
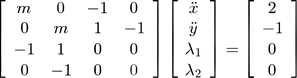 (11)
(11)
The solutions are
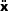 = (0,0) and Λ = (-2,-1). The
particle does not move during this time step because
= (0,0) and Λ = (-2,-1). The
particle does not move during this time step because
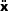 and
and
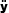 are null. But, since λ1
and λ2
are both negative, their
corresponding constraints are moved to
are null. But, since λ1
and λ2
are both negative, their
corresponding constraints are moved to
 -. This means
that, for the next time step, the system will be free of any
constraints. As the force remains constant, the next value
of
-. This means
that, for the next time step, the system will be free of any
constraints. As the force remains constant, the next value
of
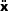 will be equal to (2m-1,-m-1). These values will
lead to an illegal position of the particle, under the line
y = 0. These computations are illustrated by the figure
2.
will be equal to (2m-1,-m-1). These values will
lead to an illegal position of the particle, under the line
y = 0. These computations are illustrated by the figure
2.
The amount of violation of the constraint g2(x) = y mainly depends on the ratio between the mass m of the particle and the intensity of the external force f. Section 5 of this paper presents the different results and comparisons.
Figure 2. (a) Since the two constraints are active, they handle by Platt′s algorithm (b) The related Lagrange multipliers are negative, the constraints are then ignored (c) The new unconstrained acceleration leads to an illegal position
The problem of Platt′s method relies on the fact that it
keeps some inequality constraints in
 + that should be
ignored. In fact, the condition gk(x) < 0 used to populate
+ that should be
ignored. In fact, the condition gk(x) < 0 used to populate
 + with inequality constraints is not well suited and an
alternative approach is proposed. A solution would be to
replace the condition gk(x) < 0 by a violation tendency
condition expressed as Jk
+ with inequality constraints is not well suited and an
alternative approach is proposed. A solution would be to
replace the condition gk(x) < 0 by a violation tendency
condition expressed as Jk
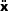 < dk
. An active constraint that
does not fulfill the violation tendency condition will be
satisfied but inactive during the next time step and does
not have to be handled.
< dk
. An active constraint that
does not fulfill the violation tendency condition will be
satisfied but inactive during the next time step and does
not have to be handled.
At the beginning of the animation, we solve equation (
1 ) to get
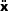 and we then populate the set
and we then populate the set
 + with the
active constraints that fulfill the violation tendency
condition. It is clear that we handle less constraints than
Platt because our criteria is more restrictive.
+ with the
active constraints that fulfill the violation tendency
condition. It is clear that we handle less constraints than
Platt because our criteria is more restrictive.
|
Algorithm 2: Platt's improved algorithm |

|
We briefly verify that this algorithm gives a correct
solution to our example illustrated in figure 1. According
to equation ( 1 ),
 = (2m-1,-m-1). The two constraints
g1
and g2
are active because x = (0,0) but only g2
fulfills
the violation tendency condition as mentioned in equation
( 12 ).
= (2m-1,-m-1). The two constraints
g1
and g2
are active because x = (0,0) but only g2
fulfills
the violation tendency condition as mentioned in equation
( 12 ).
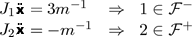 (12)
(12)
In this special case, equation ( 6 ) becomes:
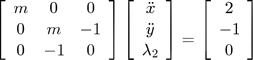 (13)
(13)
The solutions of the linear system ( 13 ) are
 (2m-1,0) and λ2 = 1. Finally, the particle will slide
along the x-axis without crossing the line y = 0 because
the constraint g1
that was not handled did not introduce a
false response.
(2m-1,0) and λ2 = 1. Finally, the particle will slide
along the x-axis without crossing the line y = 0 because
the constraint g1
that was not handled did not introduce a
false response.
This new algorithm seems to manage multiple inequality constraints in a good way, but we could highlight a problem with this method by using the same example illustrated in figure 1 with a new external force f = (-1,-2).
Figure 3. (a) The two constraints are handled since they are active (b) According to the violation tendency condition, only the constraint g2 still handled (c) The newly computed constrained acceleration leads to an illegal position
At the beginning, since x = (0,0), the constraints g1
and g2
are active. From equation ( 1 ), we obtain that
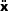 -m-1,-2m-1
, and from equation ( 14 ) that only
the constraint g2
is handled.
-m-1,-2m-1
, and from equation ( 14 ) that only
the constraint g2
is handled.
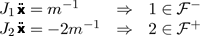 (14)
(14)
According to equation ( 14 ), we build the linear system ( 15 ).
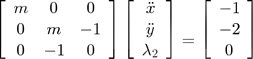 (15)
(15)
The solutions are
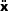 = (-m-1,0) and λ2 = 2. After the
update of x and
= (-m-1,0) and λ2 = 2. After the
update of x and
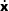 , the particle slides through the plane
defined by the constraint g1
and reaches an illegal state.
This is due to the fact that the Lagrange multiplier λ2
pushes the system in an illegal state according to the
constraint g1
, which was not previously inserted in equation ( 6 ) as it did not satisfy the violation tendency
criterion. These computations are again illustrated by the
figure 3 .
, the particle slides through the plane
defined by the constraint g1
and reaches an illegal state.
This is due to the fact that the Lagrange multiplier λ2
pushes the system in an illegal state according to the
constraint g1
, which was not previously inserted in equation ( 6 ) as it did not satisfy the violation tendency
criterion. These computations are again illustrated by the
figure 3 .
The use of the violation tendency condition Jk
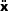 < dk
improves simultaneous active constraints management,
since only the appropriate inequality constraints are
handled by equation ( 6 ). But we have seen, from the
second example, that it is not sufficient to produce a
consistent configuration. In fact, the constraints from
< dk
improves simultaneous active constraints management,
since only the appropriate inequality constraints are
handled by equation ( 6 ). But we have seen, from the
second example, that it is not sufficient to produce a
consistent configuration. In fact, the constraints from
 +
that fulfill the violation tendency condition will produce a
vector Λ of Lagrange multipliers that prevent the system
from being in an illegal configuration according to these
handled constraints. In the meantime, the constrained
accelerations
+
that fulfill the violation tendency condition will produce a
vector Λ of Lagrange multipliers that prevent the system
from being in an illegal configuration according to these
handled constraints. In the meantime, the constrained
accelerations
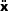 of the system could lead to an illegal
configuration according to some constraints in
of the system could lead to an illegal
configuration according to some constraints in
 -. The
only way to deal with this problem is to use the newly
computed constrained accelerations to test if the active
inequality constraints gk
(where k ∈
-. The
only way to deal with this problem is to use the newly
computed constrained accelerations to test if the active
inequality constraints gk
(where k ∈
 -) fulfill the
violation tendency condition and have to be handled. We
then need to introduce an iterative process that computes
the accelerations and checks if a previously ignored
constrained must be handled or not according to the
violation tendency condition evaluated with the newly
computed constrained accelerations. This process
is repeated until the sytem reaches the appropriate
state.
-) fulfill the
violation tendency condition and have to be handled. We
then need to introduce an iterative process that computes
the accelerations and checks if a previously ignored
constrained must be handled or not according to the
violation tendency condition evaluated with the newly
computed constrained accelerations. This process
is repeated until the sytem reaches the appropriate
state.
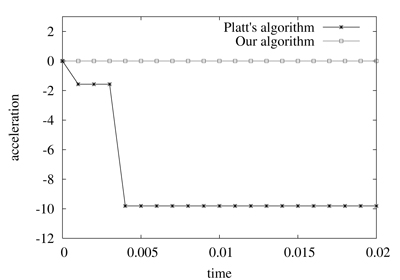
Figure 4. Comparison of Platt's algorithm and our method using the example illustrated in figure 1 with a mass m = 2. The numerical values correspond respectively to position and acceleration along the y-axis
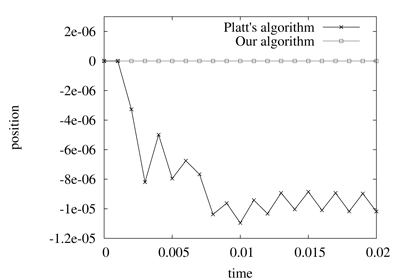
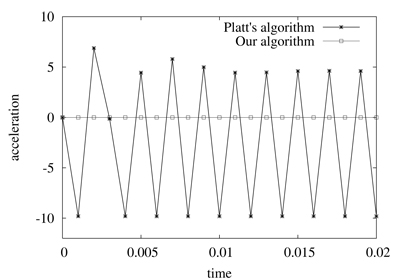
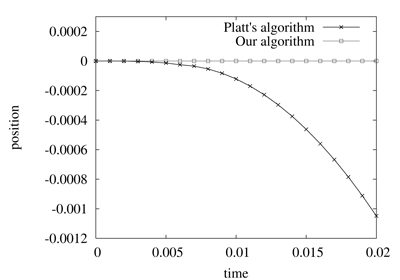
Figure 5. Comparison of Platt's algorithm and our method using the example illustrated in figure 1 with a mass m = 3. The numerical values correspond respectively to position and acceleration along the y-axis
We propose a simple and efficient solution to the
inequality constraints handling problem. At the beginning
of each time step, all active inequality constraints gk
are
detected, and
 + is emptied. We then begin an iterative
process that runs until there is no new insertion in
+ is emptied. We then begin an iterative
process that runs until there is no new insertion in
 +.
The constrained accelerations
+.
The constrained accelerations
 > are computed from
equation ( 6 ) and the violation tendency condition
Jk
> are computed from
equation ( 6 ) and the violation tendency condition
Jk
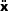 < dk
is tested on each active inequality constraint.
For any inequality constraint gk
that fulfills the condition,
we insert its index k in
< dk
is tested on each active inequality constraint.
For any inequality constraint gk
that fulfills the condition,
we insert its index k in
 + and start another iterative
step.
+ and start another iterative
step.
Since we begin with no constraints and that only
appropriate inequality constraints are inserted to
 + during
the iterative process, the last computation of
+ during
the iterative process, the last computation of
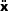 and Λ from
equation ( 6 ) will lead to an accurate configuration of
the system. Moreover, this process guarantees the
convergence towards a consistent configuration as we
begin from an empty
and Λ from
equation ( 6 ) will lead to an accurate configuration of
the system. Moreover, this process guarantees the
convergence towards a consistent configuration as we
begin from an empty
 + and only add new constraint
indices in
+ and only add new constraint
indices in
 +.
+.
In a recent communication [ RF06 ], Raghupathi presented a method also based on Lagrange multipliers. For realtime considerations, they do not allow the dynamic engine to rewind time to get back to the first constraint activation. They have to manage constraints at the end of the time step, trying to find the right accelerations to ensure constraints fulfillement. They also confess that this process is not guaranteed to converge for a given situation.
We will now compare the results obtained with Platt′s algorithm and our method, using the example illustrated in figure 1. Figure 4 and 5 illustrate a comparison of the positions and accelerations along y-axis of a particle of mass m = 2 and m = 3. We recall that the inequality constraint g2 forbids negative values for y and that the constant force f applied to the particle is equal to (2,-1).
As shown on figure 4, Platt's algorithm holds the particle in the corner at the first time step, and releases it atthe next time step. As a consequence, the particle evolves in an illegal state during the following steps. With a mass m = 2, the error related to the position is less than 10-5 with an oscillating acceleration (right column). But if we set the mass m to 3, as shown in the figure 5, errors are much more important, and the particle crosses the line y = 0 modeled by the constraint g2 .
As illustated, our algorithm keeps the particle along the x-axis within a controlled numerical error value, that is less than 10-8 in these examples.
To illustrate multiple contact constraints, we have set a billiard scene composed of 10 fixed balls placed in a corner and a moving ball that slides towards them. For each ball, we define two inequality constraints according to the corner and one inequality constraint for each pair of balls based on their in-between distance. This example is finally composed of 11 balls and 77 inequality constraints (figure 6).
Figure 6. A billiard game session illustrating our algorithm for constraints management (11 balls and 77 inequality constraints).








It is rather difficult to compare the computation times of Platt's algorithm and ours since the simulations made of simultaneous active constraints are not well handled by Platt's algorithm and produce corrupted numerical values that can lead to infinite loops. But it is quite clear that in the worst case, our method may solve n linear systems of increasing size where n is the total number of inequality constraints. The complexity of our solution is then higher than Platt's algorithm. But we recall that our main contribution is not to speed up an existing method but to propose a reliable algorithm mainly dedicated to off-line simulations.
In this paper, we presented a novel algorithm to manage simultaneous active inequality constraints. Among all the existing methods to handle constraints within a physically-based animation, we focused on the Lagrange method which provides a reliable way to ensure that constraints are always exactly fulfilled. But, in the special case of several active inequality constraints, we have to take care on how to handle these simultaneous constraints. Platt proposed an algorithm based on Lagrange multipliers but we showed that this method is unable to solve even simple examples. We then explained how to improve this algorithm in order to propose a new reliable and efficient method for inequality constraints handling. Beyond the example illustrated in figure 1, we produced a short movie simulating a billiard game. Some snapshots are gathered in figure 6.
[Arn89] Mathematical Methods of Classical Mechanics, 1989, , Graduate Texts in Mathematics, Springer Verlag, New York, 2nd Edition, isbn 0-387-96890-3.
[Bar93] Non-penetrating rigid body simulation, State of the Art Reports, Eurographics '93, September 1993, Barcelona, Spain.
[Bau72] Stabilization of constraints and integrals of motion in dynamical systems, Computer Methods in Applied Mechanics and Engineering, (1972), 1—16, issn 0045-7825.
[BB88] A modeling system based on dynamic constraints, SIGGRAPH '88: Proceedings of the 15th annual conference on Computer graphics and interactive techniques, 1988, ACM Press, New York, NY, USA, pp. 179—188, isbn 0-89791-275-6.
[Bjo96] Numerical Methods for Least Squares Problems, SIAM, Philadelphia, Penn., 1996, isbn 0-89871-360-9.
[Gol80] Classical Mechanics, 1980, 2nd Edition, Addison-Wesley, Reading, MA, U.S.A., isbn 0-321-18897-7.
[NW00]
Numerical Optimization,
New York,
Springer,
2000,
[Pla92] A Generalization of Dynamic Constraints, CVGIP: Graphical Models and Image Processing, (1992), no. 6, 516—525, Academic Press, Inc., issn 1049-9652.
[RF06] QP-Collide: A New Approach to Collision Treatment, Journées du groupe de travail Animation et Simulation (GTAS), Annual French Working group on Animation and Simulation, pp. 91—101, June 2006, Institut de Recherche en Informatique de Toulouse.
[TKZ05] Collision Detection for Deformable Objects, Computer Graphics Forum, (2005), no. 1, 61—81, issn 0167-7055
[TPB89] Physically-based modeling: past, present, and future, SIGGRAPH '89: ACM SIGGRAPH 89 Panel Proceedings, 1989, Boston, Massachusetts, United States, pp. 191—209, ACM Press, New York, NY, USA, isbn 0-89791-353-1.
[VF02] Numerical Recipes in C++: The Art of Scientific Computing, 2nd Edition, William H. Press and Saul A. Teukolsky (Eds.), Cambridge University Press, Cambridge (UK) and New York, 2002, isbn 0-521-75033-4.
Volltext ¶
-
 Volltext als PDF
(
Größe:
9.1 MB
)
Volltext als PDF
(
Größe:
9.1 MB
)
Lizenz ¶
Jedermann darf dieses Werk unter den Bedingungen der Digital Peer Publishing Lizenz elektronisch übermitteln und zum Download bereitstellen. Der Lizenztext ist im Internet unter der Adresse http://www.dipp.nrw.de/lizenzen/dppl/dppl/DPPL_v2_de_06-2004.html abrufbar.
Empfohlene Zitierweise ¶
Antoine Jonquet, Olivier Nocent, and Yannick Remion, The art to keep in touch: The ''good use'' of Lagrange multipliers. JVRB - Journal of Virtual Reality and Broadcasting, 4(2007), no. 15. (urn:nbn:de:0009-6-12767)
Bitte geben Sie beim Zitieren dieses Artikels die exakte URL und das Datum Ihres letzten Besuchs bei dieser Online-Adresse an.