GRAPP 2006
High level methods for scene exploration
extended and revised for JVRB
urn:nbn:de:0009-6-11144
Abstract
Virtual worlds exploration techniques are used in a wide variety of domains — from graph drawing to robot motion. This paper is dedicated to virtual world exploration techniques which have to help a human being to understand a 3D scene. An improved method of viewpoint quality estimation is presented in the paper, together with a new off-line method for automatic 3D scene exploration, based on a virtual camera. The automatic exploration method is working in two steps. In the first step, a set of “good” viewpoints is computed. The second step uses this set of points of view to compute a camera path around the scene. Finally, we define a notion of semantic distance between objects of the scene to improve the approach.
Keywords: Scene understanding, automatic virtual camera, good point of view
Subjects: Camera
One of the reasons for rapid development of computer science was the introduction of human-friendly interfaces, which have made computers easy to use and learn. The increasing exposure of the general public to technology means that their expectations of display techniques have changed. The increasing spread of the internet has changed expectations of how and when people are to access information. As a consequence, a lot of problems arose. One of them is the automatic exploration of a virtual world. In recent years, people pay essentially more attention to this problem. They realized the necessity of fast and accurate techniques for better exploration and clear understanding of various virtual worlds. A lot of projects use results of intelligent camera placement research, from the “virtual cinematographer” [ HCS96 ] to motion strategies [ MC00 ].
In Computer Graphics a lot of efforts are focused on improving quality and realism of renders, but rarely one focuses on the interaction and modeling. Indeed, usually, the user must choose viewpoints himself to better inspect and even to understand what a scene looks like. The goal of this work was the developing of new techniques for automatic exploration of virtual worlds.
Quality of a view direction is a rather intuitive term and, due to its inaccuracy, it is not easy to precise for a selected scene, which viewpoints are “good” and which are not. Over the last decades, many methods were proposed to evaluate quality of view directions for a given scene and to choose the best one. All of them are based on the fact that the best viewpoint gives the user maximum amount of information about a scene. And again, an imprecise term “information” is met.
This paper is organized as follows: section 2 gives a brief description of previous works. A new method of viewpoint quality estimation is described in section 3 . A new method of global scene exploration is presented in section 4 . Section 5 shows how Artificial Intelligence techniques could be used in the domain of automatic exploration. Finally, section 6 concludes our work and points out directions of future work.
As we have mentioned above, due to advances in information technologies, the importance of crafting best views has grown. The key-role in the domain of automatic explorations belongs to estimating viewpoint quality procedure, so, we start with reviewing advances in this domain.
A number of papers have addressed the problem of automatically selecting a viewpoint that maximally elucidate the most important features of an object.
The first works on visual scene understanding were published at the end of the years 80s. Kamada and Kawai [ KK88 ] have proposed a fast method to compute a point of view, which minimizes the number of degenerated edges of a scene (refer to figure 1 ). They consider a viewing direction to be good if parallel line segments lie in a projection as far away from each other as possible. Intuitively, the viewer should be as orthogonal to every face of the 3D object as possible. As this is hard to realize, they suggest to minimize the maximum angle deviation (over all the faces) between a normal to the face and the line of the viewer's sight.
The technique is interesting for small wire-frame models, but it is not very useful for more realistic scenes. Since this technique does not take into account which parts of the scene are visible, a big element of the scene may hide all the rest in the final image. Plemenos and Benayada [ PB96 ] have proposed a heuristic that extends the definition given by Kamada and Kawai. The heuristic considers a viewpoint to be good if it gives a high amount of details in addition to the minimization of the deviation. Thus, the function is the percentage of visible polygons plus the percentage of used screen area.
Stoev and Straßer in [ SS02 ] consider a different approach that is more suitable to viewing terrains, in which most surface normals in the scene are similar, and visible scene depth should be maximized.
Sbert et al. [ SFR02 ] introduced an information theory-based approach to estimate the quality of a viewpoint. To select a good viewpoint they propose to maximize the so called “viewpoint entropy”. The function is the Shannon's entropy, where projected areas of faces are taken as a discrete random variable. Thus, the maximum entropy is obtained when a certain point can see all the faces with the same relative projected area. By optimizing the value of entropy in images, Sbert et al. try to capture the maximum number of faces under the best possible orientation.
Recently Chang Ha Lee et al. [ LVJ05 ] have introduced the idea of mesh saliency as a measure of regional importance for graphics meshes. They define mesh saliency in a scale-dependent manner using a center-surround operator on Gaussian-weighted mean curvatures. The human-perception-inspired importance measure computed by the mesh saliency operator gives more pleasing resultsin comparison with purely geometric measures of shape, such as curvature.
Blanz et al. [ BTB99 ] have conducted user studies to determine the factors that influence the preferred views for 3D objects. They conclude that selection of a preferred view is the result of complex interactions between task, object geometry, and object familiarity.
A single good point of view is generally not enough for complex scenes, and even a list of good viewpoints does not allow the user to understand a scene, as frequent changes of viewpoint may confuse him (her). To avoid this problem, dynamic exploration methods were proposed.
Barral et al. and Dorme [ BDP00, Dor01 ] proposed a method, where a virtual camera moves in real time on the surface of a sphere surrounding the virtual world. The scene is being examined in incremental manner during the observation. In order to avoid fast returns of the camera to the starting position, the importance of a viewpoint is made inversely proportional to the distance along the camera path from the starting to the current position.
Vázquez and Sbert [ VS03 ] propose an automatic method of indoor scene exploration with limited degrees of freedom (in order to simulate a human walk-through). The method is based on the viewpoint entropy.
In [ MC00, VFSH02 ] image-based techniques are used to control the camera motions in a changing virtual world. The problem faced in the paper is the adaptation of the camera behavior to the changes of the world.
For more details, a state of the art paper on virtual world global exploration techniques is available [ PS06 ].
Although the above methods of viewpoint quality estimation allow to obtain interesting results, they are low-level methods, as they use inadequate “vocabularies”. Let us consider an example. The scanning process at 300 dpi resolution produces about 9 megapixels per A4 page. However, nobody uses elementary pixel configuration to describe content and structure of this page. Instead, people apply Optical Character Recognition methods and represent content by characters and structural markup. Computer Graphics suffers from weak representation of 3D data. Development of proper “vocabularies” for a new generation of meta-data, able to characterize content and structure of multimedia documents, is a key-feature for categorization, indexing, searching, dissemination and access. It would be a grand challenge if a complete semantic 3D model could be used instead of projection in lower dimensions (image, text, animations) or structureless collection of polygons.
Thus, while these low-level methods work good in estimating viewpoint quality of a single object, they often fail in complex scenes. In this section the first high-level method is presented. The main idea of the method is to pass to higher level of perception in order to improve the notion of viewpoint quality. Let us suppose that, having a complex scene, there exists some proper division of the scene into a set of objects. Figure 2 presents an example of such a scene, where the subdivision into a set of objects is shown by different colors. These objects are: the computer case, the display, the mouse, the mouse pad, two cables, the keyboard and several groups of keys.
Figure 2. The scene is subdivided into a set of objects. The display is almost completely hidden by the case, but we could clearly recognize it.

Only 20% of the display surface is visible, but it does not embarrass its recognition because, if we are familiar with the object, we could predict what does it look like. Thus, we conclude that if there exists a proper subdivision of a scene into a set of objects, the visibility of the objects could bring more information than just the visibility of the faces, and this leads us to the new level of abstraction.
This method of viewpoint quality estimation makes the first few steps in the direction of semantic description of a 3D scene. Note that developing innovative ways to represent a scene originates a lot of problems such as conversion of already existing scenes to new format. However, the requirement of a scene division into a set of objects does not limit the area of the method application. There are many ways to get it. First of all, complex scenes often consist of non-adjacent simple primitives, and this leads to the first disjunction of a scene. Otherwise, if a scene (or some parts of a scene) is represented by a huge mesh, it could be decomposed. The domain of the surface decomposition is well-studied and there are a lot of methods giving excellent results. One can point at results of Zuckerberger et al. [ ZTS02 ] and Chazelle et al. [ CDST95 ].
The method we propose is also useful in declarative modelling by hierarchical decomposition (refer to [ Ple95 ] for the main principles). In such a case, the decomposition could be provided by a modeler directly, or it can be combined with the information extracted from the scene geometry.
The main idea is to define how pertinent each object is and how well it is predictable. Then for any viewpoint we can determine visible parts of the scene. With this information given we can calculate how well each object is observed. The total viewpoint quality consists of the sum of observation qualities for each object.
An accurate definition of the new heuristic is given further. Let us suppose that for each object ω of a scene Ω its importance q(ω) : Ω → R+ is specified.
We would like to generalize the method and do not want to be limited by a strict definition of the importance function, because it could be done in different ways, especially, if some additional knowledge about a scene is supplied. For example, if the method is incorporated into some dedicated declarative modeler, the importance of an object could be assigned in dependence on its functionality. Moreover, after the first exploration the importances could be rearranged in a different manner to see various parts of a scene more precisely than during the previous exploration.
If no additional information is provided and the user takes into account scene geometry only, then the size of object bounding box could be considered as the importance function:
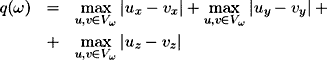
, where Vω is the set of vertices of the object ω.
It is also necessary to introduce a parameter characterizing the predictability (or familiarity) of an object: ρω : Ω → R+ . In other words, the parameter determines the quantity of object surface to be observed in order to well understand what the object looks like. If an object is well-predictable, then the user can recognize it even if he sees a small part of it. Bad predictability forces the user to observe attentively all the surface.
The ρω parameter sense could be also interpreted in a different manner. Even if an object is well-predictable (for example, it is a famous painting), the parameter ρω could be chosen as for an object with bad predictability. This choice forces the camera to observe all the painting.
We propose to consider the function
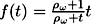 as
the measure of observation quality for an object with
predictability ρω
, where 0 ≤ t ≤ 1 is the explored
fraction of the object (for example, the area of the
observed surface divided by the total area of the object
surface). Refer to figure 3 for an illustration. If the
percentage t for the object ω is equal to zero (the user has
not seen the object at all), then f(t) is zero (the user
cannot recognize the object). If all the surface of the
object ω is observed, then f(t) is 1, the observation is
complete.
as
the measure of observation quality for an object with
predictability ρω
, where 0 ≤ t ≤ 1 is the explored
fraction of the object (for example, the area of the
observed surface divided by the total area of the object
surface). Refer to figure 3 for an illustration. If the
percentage t for the object ω is equal to zero (the user has
not seen the object at all), then f(t) is zero (the user
cannot recognize the object). If all the surface of the
object ω is observed, then f(t) is 1, the observation is
complete.
Figure 3. The behavior of the function 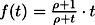 for two values of the parameter ρ. (a) ρ = 0.1, even
a part of an object provides a good knowledge. (b)
ρ = 1000, the user should see all the object to get a
good knowledge.
for two values of the parameter ρ. (a) ρ = 0.1, even
a part of an object provides a good knowledge. (b)
ρ = 1000, the user should see all the object to get a
good knowledge.
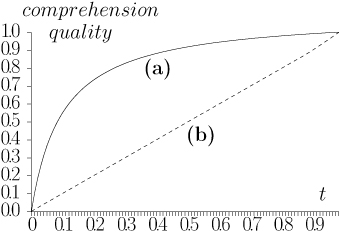
If nothing is known about a scene except its geometrical representation, then one may suppose that the scene does not contain extraordinary (very rough) topology. Then the parameter ρ could be taken as rather small value, for example, ρω ≡ 0.1 ∀ ω ∈ Ω. In such a case even exploration of a part of an object gives a good comprehension.
Now let us suppose that there exists some additional knowledge, for example, a virtual museum is considered. Then for all the paintings the parameter could be taken equal to 1000 and, for all the walls, chairs, doors equal to 0.1. Now, in order to get a good comprehension of a painting, one should observe all its surface, but only a small part of door or wall is necessary to recognize them.
Let us consider a viewpoint p. For scene objects this point gives a set of values Θ(p) = {0 ≤ θp,ω ≤ 1,ω ∈ Ω}, where θp,ω is the fraction of visible area for the object ω from the viewpoint p. θp,ω = 0 if the object is not visible and θp,ω = 1 if one can see all its surface from the viewpoint p.
The fraction θp,ω may be computed in various ways. The simplest one is to divide the area of the visible surface by the total area of an object. Another way is to divide the curvature of the visible surface by the total curvature of the object. In both cases, we obtain the fraction equal to 0 if an object is not visible at all and equal to 1 if we could see all its surface.
Thus, we propose to evaluate the viewpoint quality as the sum of scene object importances with respect to their visibility and predictability:
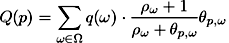 (1)
(1)
Figure 4 shows the behaviour of two viewpoint quality heuristics. The mean curvature is taken as the first one, while the high-level heuristic, proposed in this section, is taken as another one. For the high-level method no additional information is provided, so, the bounding box sizes are taken as the importance function q(ω) and ρω ≡ 0.1∀ ω ∈ Ω.
Figure 4: The qualities for 100 viewpoints equally distanced from the center of the model. The best view directions are indicated by the black sectors. (a) Mean curvature; (b) the high-level heuristic.
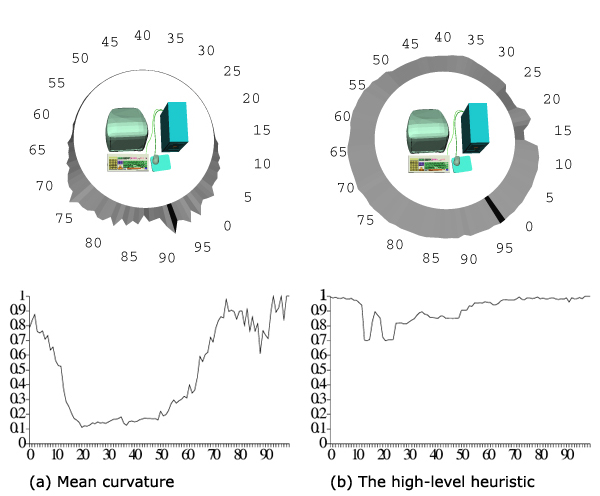
The best viewpoints, chosen by the two methods, are quite close (the picture is shown in figure 5 ), but there are significant differences in the estimation of other view directions.
Let us compare figure 2 , showing the scene from the viewpoint number 10, and figure 5 , showing it from the best viewpoint. It is clear that the viewpoint 10 is less attractive, but it still gives a good representation of the scene. The function on figure 4(b) decreases smoothly in this region, while figure 4(a) shows a drastic fall. At the viewpoint 17 the function from figure 4(b) grows, because the back side of the display and a part of the keyboard are visible simultaneously. Then it decreases again because the case covers the keyboard. The high-level method also shows a better quality than the low-level one from the back side of the scene. From each viewpoint some parts of the mouse or of the keyboard are visible, so the estimation should not be as small as at figure 4(a) .
The viewpoint quality estimation is only the first step in the domain of scene understanding. In order to help a user to get a good knowledge of a scene, methods, allowing to choose the best viewpoint (or a set of viewpoints), should be proposed. Dynamic exploration methods could be very helpful too, since a set of static images is often not sufficient for understanding of complex scenes.
There are two classes of methods for virtual world exploration. The first one is the global exploration class,where the camera remains outside the explored world. The second class is the local exploration one. In this class the camera moves inside a scene and becomes a part of the scene. Local exploration may be useful and even necessary in some cases, but only global exploration could give the user a general knowledge on a scene. In order to simplify the presentation, we present a method of global exploration of fixed unchanging virtual worlds. The method can be adapted to perform local explorations. The only difficulty is the collisions detection. It can be solved introducing displacement maps for the camera.
Thus, let us suppose that a scene is placed in the center of the sphere, whose discrete surface represents all possible points of view. Having the viewpoint quality criterion and a rapid algorithm for visibility computations (refer to [ SP05 ]), we are ready to choose good views. The main idea of the method is to find a set of viewpoints, giving a good representation of a scene, and then to connect the viewpoints by curves in order to get a simple path on the surface of the sphere, the trajectory of the camera.
As the viewpoint quality measure we use equation (1). The heuristic is very flexible and gives good results even (and especially) for complex scenes. The viewpoints should be as good as possible (provide as much information as possible) and the number of viewpoints should not be very great. These criteria are satisfied with a greedy search scheme. Firs of all, we define the quality of a set of viewpoints. Then, starting from the best viewpoint, at each step we find the best viewpoint for the unexplored part of the scene. The algorithm stoppes when the quality of the set surpasses the desirable level of the comprehension.
Let us suppose that the scene Ω consists of separated
meshes {ω1,...,ωnΩ
}. The sets of vertices V and viewpoints
P are provided.
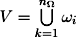 , k ≠ l ⇒ ωl ∩ ωk = ∅. For
each viewpoint p of the discrete sphere P the set of visible
vertices V(p) ⊆ V is given.
, k ≠ l ⇒ ωl ∩ ωk = ∅. For
each viewpoint p of the discrete sphere P the set of visible
vertices V(p) ⊆ V is given.
Now let us extend the definition given by equation (1) and define the quality of a set of views (photos). Let us suppose we have selected a set of viewpoints P1 from the all possible camera positions P. Each object ω of the scene may be visible from multiple viewpoints, so it is necessary to determine its visible part θP1,ω .
Let us denote the curvature in a vertex v ∈ V as
C(v) and the total curvature of a mesh V1 ⊆ V as 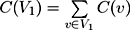 . Then for a given object ω its visible
fraction θP1,ω
equals to the curvature of visible part
divided by the total curvature of the object's surface.
Therefore,
. Then for a given object ω its visible
fraction θP1,ω
equals to the curvature of visible part
divided by the total curvature of the object's surface.
Therefore, 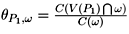 ,
,
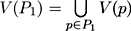 . Of
course, we suppose here that all the objects in Ω have
non-zero curvatures.
. Of
course, we suppose here that all the objects in Ω have
non-zero curvatures.
Once we have determined which parts of every object are visible from our set of viewpoints P1 , the quality equation remains the same:
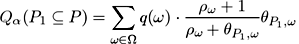
As we have mentioned before, a set of views, giving a good representation of a scene, could be obtained by a greedy search. The greediness means choosing a best viewpoint at each step of the algorithm. Starting from the best viewpoint, at each step we find the best viewpoint for the unexplored part of the scene. The algorithm stoppes when the quality of the set surpasses the desirable level of the comprehension.
More strictly: having given a threshold 0 ≤ τ ≤ 1 (the
desirable level of the comprehension), one should
find a set of viewpoints Mk ⊆ P such as
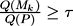 .
Here Q(Mk) means observation quality for the set of
viewpoints Mk
, and is the observation quality for
the set of all possible viewpoints.
At the beginning M0 = ∅, each step i of the algorithm
adds to the set the best view pi. Mi = Mi-1 ∪ {pi}:
.
Here Q(Mk) means observation quality for the set of
viewpoints Mk
, and is the observation quality for
the set of all possible viewpoints.
At the beginning M0 = ∅, each step i of the algorithm
adds to the set the best view pi. Mi = Mi-1 ∪ {pi}:
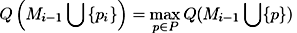
The next question is: if there are two viewpoints and the camera has to move from one to another, which path is to be chosen? A naive answer is to connect the viewpoints with the shortest path (geodesic line). But it does not guarantee that the path consists of good viewpoints. Let us consider factors influencing the quality of a film.
We suppose that the resulting distance function is the superposition of different costs and discounts. First of all, one must take into account the cost of moving cm the camera from one point to another (proportional to the Euclidian distance). The cost of camera turns may be discarded as the camera moves are restricted to the sphere.
Now let us introduce the discount cq
that forces
the camera to pass via “good” viewpoints. The main
idea is to make the distances vary inversely to the
viewpoint qualities. For example, it can be done in
the following way: if two viewpoints p1
and p2
are
adjacent in a sphere tessellation, then the new distance
between p1
and p2
is calculated with the formula:
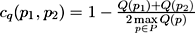 . This empiric formula
augments displacement costs between “bad” viewpoints
and reduces near “good” ones.
. This empiric formula
augments displacement costs between “bad” viewpoints
and reduces near “good” ones.
Thus, the resulting distance function between two adjacent viewpoints is:
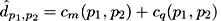 (2)
(2)
Figures 6 and 7 illustrate the idea. It is easy to see that the camera trajectory presented at figure 7(b) brings to a user more information than the shortest one.
Figure 6. The reason to change the metric. The circles represent viewpoints: larger circles denote better viewpoints. The solid line shows the geodesic line between viewpoints A and B, the dashed line shows the shortest path according to the new metric. It is clear that sometimes it would be better to increase the length of the walk-trough in order to better inspect certain places.
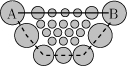
Figure 7. The trajectories between two selected points on the surface of the surrounding sphere. (a) Shortest line connecting two viewpoints. (b) Shortest line with respect to the viewpoint qualities.
Now, having defined the metric and having found the set of viewpoints, we would like to determine a trajectory of the camera. It is not hard to construct a complete graph of distances G = (Mk,E), where the weight of an arc (v1,v2) ∈ E is equal to the metric between the viewpoints v1 and v2 (equation ( 2 )).
Now the trajectory could be computed as the shortest Hamiltonian path (or circuit, if we would like to return the camera to initial point). The problem is also known as the travelling salesman problem (TSP). Unfortunately, the TSP problem is NP-complete even if we require that the cost function satisfies the triangle inequality. But there exist good approximation algorithms to solve the problem. Moreover, often |Mk | is rather small, and the problem in such a case could be solved even by the brute-force algorithm in real-time.
Now we can compute a broken line as the camera trajectory. However, brusque change of direction in vertices of the line may be disattracting. The simple solution is to calculate a spline with the line vertices as control points.
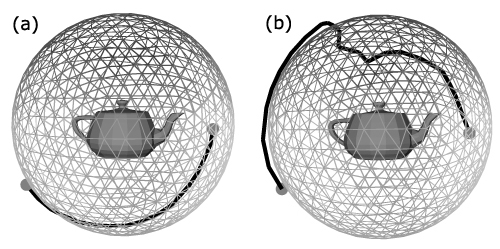
Figures 8 and 9 show camera trajectories for the Utah teapot model. The first one is obtained by applying the incremental technique with the viewpoint entropy as the quality heuristic, and the second one is obtained by our method.
Figure 8. The exploration trajectory for the Utah teapot model. The trajectory is computed by the incremental method using the viewpoint entropy as the quality heuristic. Images are taken consequently from the “movie”. The first one is the best viewpoint.
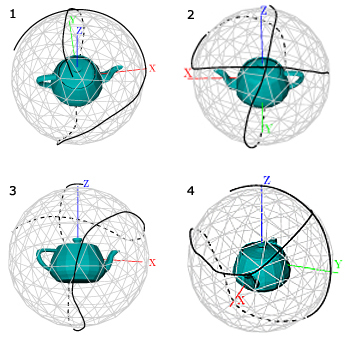
Figure 9. The exploration trajectory for the Utah teapot model, obtained with the new technique. Images are taken consequently from the “movie”. Black knots are the control points of the trajectory, i.e. an approximation of the minimal set of viewpoints sufficient to see all the surface of the teapot model.
Both of them show 100% of the surface of the teapot model. The new method could give brusque changes of the trajectory, and the old one is free of this disadvantage. A simple way to smooth the trajectory is to construct a NURBS curve. Control points for the curve are to be taken from the approximation of the minimal set of viewpoints, and its order is to be defined by solving the TSP task. The new technique gives significantly shorter trajectories, and this advantage is very important.
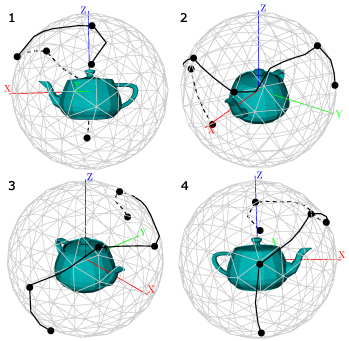
The next example of the new method application is shown at figure 10 . This model is very good for testing exploration techniques, it represents six objects imposed into holes on the sphere, and the explorer should not miss them. None of the previously proposed methods can properly observe this model. All of them, having found an embedded object, are confused in choosing the next direction of movement. This happens because of missing information about unexplored areas. On the contrary, the new method operates with the analytic visibility, allowing to determine where some unexplored areas rest.
Figure 10. The exploration trajectory for the sphere with several embedded objects. Images are taken consequently from the “movie”, black knots are the control points of the trajectory.
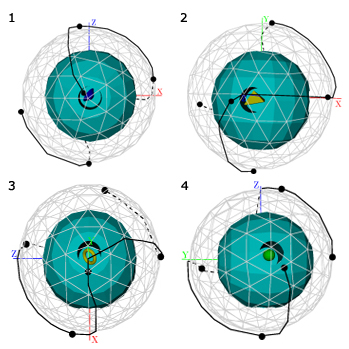
As we have mentioned above, it would be very helpful if a semantic 3D model could be used instead of structureless collection of polygons. Let us consider an example (see figure 11 ). Figure 11(a) shows a scene with two churches. There are three manually fixed viewpoints. The dashed line is the trajectory, obtained by the above method of exploration, adapted to indoor explorations. The exploration is started at the viewpoint 1. It is easy to see that the camera turns aside from the big church in the viewpoint 2 and then reverts back again. The trajectory is very short and smooth, but the exploration is confusing for the user.
Figure 11. Two different trajectories. (a) During traversal from the point 1 to 3 the camera turns aside from the big church and then reverts back again. (b) The camera turns aside from the big church only when its exploration is complete.
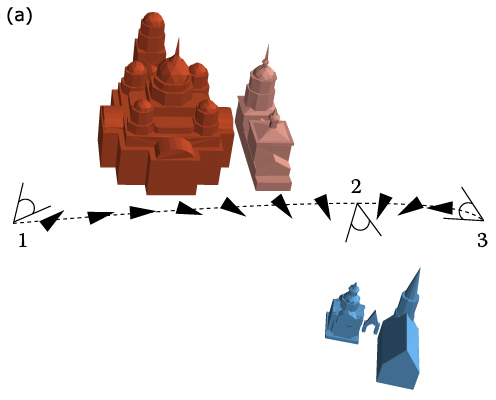
Figure 11(b) shows another trajectory, where the exploration starts in the viewpoint 1, passes via 3 and terminates in the point 2. The camera turns aside from the big church only when its exploration is complete. Despite the increased length of the trajectory, the exploration is more clear.
Thus, we postulate that the above method of automatic exploration could be improved by regrouping the control frames in dependence on relativeness of information they show. In other words, if two frames show the same object, they are to be consequent in the final animation.
The relativeness (or semantic distance) can be defined in many ways. For example, Foo et al. in [ FGRT92 ] define a semantic distance in conceptual graphs based on Sowa's definition. Zhong et al. in [ ZZLY02 ] propose an algorithm to measure the similarity between two conceptual graphs.
In our work we use semantic networks. An example of such a network is given at figure 12 .
Figure 12. The semantic network example for a virtual museum. Importances of relationships are denoted by thickness of lines.
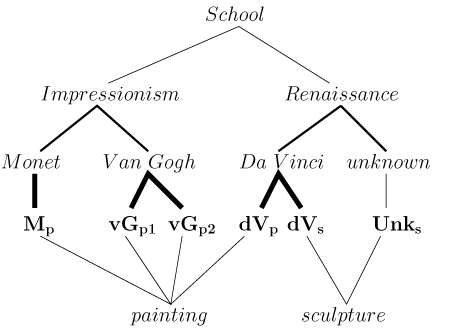
The figure shows a semantic network for a small virtual museum, which contains paintings by Van Gogh (vGp1, vgp2), Monet (Mp), Da Vinci (dVp) and two sculptures by Da Vinci (dVs) and unknown sculptor (Unks). Importances of relationships are denoted by thickness of lines. Thus, the information that Mp is created by Claude Monet is more important than the information that Mp is a painting.
In order to measure semantic distance between two objects s and t, we transform the semantic network to an undirected flow network G = (C,EC). Edges EC correspond to relationships between concepts C of the semantic network, capacities b(i,j) > 0 ∀(i,j) ∈ EC are to be set according to the relationship importances. s and t are the source and the sink with unbounded supply and demand, respectively. Let us denote the capacity of an xy-cut (x,y ∈ C) as cut(x,y) and the capacity of xy-mincut as mincut(x,y). Then the semantic distance can be defined as follows:
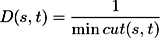 (3)
(3)
For continuity reasons we define D(x,y) ≡ 0 ∀x ∈ C. It is easy to see that equation ( 3 ) defines a metric D : C x C → R+ .
Now, having defined the semantic distance between two objects, we can introduce the semantic distance between two “photos”. More strictly, if one “photo” shows a set of objects A ⊆ C and another shows a set of objects B ⊆ C, one can define the similarity distance between the sets as follows:
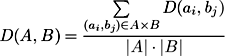
The distance between sets is also a metric.
Now let us show how the metric could be used in scene exploration. In the previous section we have constructed a complete weighted graph G. We redefine the travelling cost between two “photos” as the length of the shortest path (equation ( 2 )) between them plus the semantic distance between the “photos”.
Figure 13(a) presents the shortest exploration trajectory for a small virtual museum we presented above. The corresponding semantic network is shown in figure 12 . The exploration starts from the Van Gogh painting (vGp1), then comes Da Vinci painting dVp, Monet (Mp) etc. The exploration terminates after visiting the second painting of Van Gogh (vGp2).
It is clear that the order is not good. For example, it is better to observe creations of one author consequently. A trajectory, obtained with respect to the semantic network is shown at figure 13(b) . The camera starts with two paintings by Van Gogh (vGp1, vGp2), continues with Monet (Mp), then shows the painting by Da Vinci (dVp), passes to the sculpture by Da Vinci (dVs) and terminates with the sculpture by unknown author (Unks).
Figure 13. The virtual museum exploration trajectories. (a) The shortest trajectory. (b) The shortest trajectory with respect to the semantic network shown at figure 12.
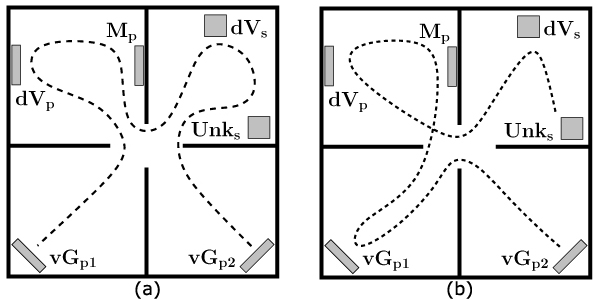
It is easy to see that the second trajectory is more logical than the first one. The trajectory does not interrupt exploration of items by the same author and the camera passes to the renaissance items only when all the impressionists paintings are explored.
In this paper a new high-level approach to evaluate viewpoint quality is presented. A non-incremental method of global scene exploration is demonstrated. It allows a camera to navigate around a model until most of interesting reachable places are visited. The method runs in real-time. In distinction from [ Dor01 ], it guarantees that all interesting places in a scene will be observed. The techniques, presented in this paper, may be generalized in order to be used in local exploration too. In order to make the generalization, it is necessary to solve the camera-objects collision problem. Figure 14 shows our preliminary results in the domain of local exploration.
Figure 14. Free navigating in 3D: the resulting trajectory is shown from two points of view: from the side and from the top. The hidden part of the trajectory is shown in the white dashed line.


A new measure of similarity between objects is also introduced in this paper. It is useful when some additional knowledge of scene structure could be provided. This measure, so called semantic distance, evaluates relationships in the scene to improve the exploration method.
Semantic networks promise to be a rich area for further research. We are currently defining similarity measure between objects, but it should be possible to extend the definitions taking into account user preferences. It will also be an interesting exercise to use machine learning techniques to take into account implicit user preferences. Different people have different tastes, and artificial intelligence techniques could help to handle some uncertainties. Probably, it would be possible to create for each user a database of preferences to improve exploration of further scenes.
The authors would like to express their gratitude towards the European Community and the Limousin Region for their financial support of the present work.
[BDP00] Scene understanding techniques using a virtual camera, Proceedings of Eurographics 2000, Short Presentations, Rendering and Visibility, Interlaken (Switzerland), August 2000.
[BTB99] What object attributes determine canonical views?, Perception (1999), no. 5, 575—600, issn 0301-0066.
[CDST95] Strategies for polyhedral surface decomposition: an experimental study, SCG’95: Proceedings of the eleventh annual symposium on Computational geometry, New York, NY, USA, ACM Press, 1995, pp. 297—305, isbn 0-89791-724-3.
[Dor01] Study and implementation of 3D scene understanding techniques, Ph.D. thesis, University of Limoges (France), June 2001, (In French).
[FGRT92] ch. Semantic distance in conceptual graphs, Conceptual structures: current research and practice, pp. 149—154 Ellis Horwood, Upper Saddle River, NJ, USA, 1992, isbn 0-13-175878-0.
[HCS96] The virtual cinematographer: a paradigm for automatic real-time camera control and directing, Proceedings of SIGGRAPH’96, Annual Conference Series, August 1996, pp. 217—224, isbn 0-89791-746-4.
[KK88] A simple method for computing general position in displaying three-dimensional objects, Computer Vision, Graphics and Image Processing (1988), no. 1, 43—56, issn 0734-189X.
[LVJ05] Mesh saliency ACM Transactions on Graphics (TOG) (2005), no. 3, 659—666, issn 0730-0301.
[MC00] Image-based virtual camera motion strategies, Graphics Interface Conference, GI’00, Montreal, Quebec, S. Fels and P. Poulin (Eds.), Morgan Kaufmann, May 2000, pp. 69—76, isbn 0-9695338-9-6.
[PB96] Intelligent display in scene modelling. New techniques to automatically compute good views, GraphiCon’96, Saint Petersburg (Russia), July 1996.
[Ple95] Declarative modeling by hierarchical decomposition. the actual state of the MultiFormes project, GraphiCon’95, Saint Petersbourg (Russia), July 1995.
[PS06] Intelligent scene display and exploration, International Conference GraphiCon’2006, Novosibirsk (Russia), July 2006.
[SFR02] Applications of the information theory to computer graphics, International Conference 3IA 2002, Limoges (France), May 2002, isbn 2-914256-04-3.
[SP05] Viewpoint quality and scene understanding, VAST 2005: Eurographics Symposium Proceedings, ISTI-CNR Pisa, Italy, Mark Mudge, Nick Ryan, and Roberto Scopigno, (Eds.), Eurographics Association, November 2005, pp. 67—73, isbn 3-905673-28-2.
[SS02] A case study on automatic camera placement and motion for visualizing historical data, VIS'02: Proceedings of the conference on Visualization'02, Washington, DC, USA, IEEE Computer Society , 2002, pp. 545—548, isbn 0-7803-7200-X.
[VFSH02] Image-based modeling using viewpoint entropy, Computer Graphics International, 2002, pp. 267—279.
[VS03] Automatic indoor scene exploration, Proceedings of 6th International Conference on Computer Graphics and Artificial Intelligence 3IA’2003, Limoges (France), May 2003, pp. 13—24.
[ZTS02] Polyhedral surface decomposition with applications, Computers & Graphics (2002), no. 5, 733—743, issn 0097-8493.
[ZZLY02]
Conceptual graph matching for semantic search,
Proceedings of the 10th
International Conference on Conceptual
Structures ICCS 2002,
London, UK,
Springer-Verlag,
2002,
pp. 92—106,
Lecture Notes in Computer Science, Vol. 2393,
isbn 3-540-43901-3.
Volltext ¶
-
 Volltext als PDF
(
Größe:
1.0 MB
)
Volltext als PDF
(
Größe:
1.0 MB
)
Lizenz ¶
Jedermann darf dieses Werk unter den Bedingungen der Digital Peer Publishing Lizenz elektronisch übermitteln und zum Download bereitstellen. Der Lizenztext ist im Internet unter der Adresse http://www.dipp.nrw.de/lizenzen/dppl/dppl/DPPL_v2_de_06-2004.html abrufbar.
Empfohlene Zitierweise ¶
Dmitry Sokolov, and Dimitri Plemenos, High level methods for scene exploration. JVRB - Journal of Virtual Reality and Broadcasting, 3(2006), no. 12. (urn:nbn:de:0009-6-11144)
Bitte geben Sie beim Zitieren dieses Artikels die exakte URL und das Datum Ihres letzten Besuchs bei dieser Online-Adresse an.