CVMP 2010
Generating Realistic Camera Shake for Virtual Scenes
urn:nbn:de:0009-6-38335
Abstract
When depicting both virtual and physical worlds, the viewer's impression of presence in these worlds is strongly linked to camera motion. Plausible and artist-controlled camera movement can substantially increase scene immersion. While physical camera motion exhibits subtle details of position, rotation, and acceleration, these details are often missing for virtual camera motion. In this work, we analyze camera movement using signal theory. Our system allows us to stylize a smooth user-defined virtual base camera motion by enriching it with plausible details. A key component of our system is a database of videos filmed by physical cameras. These videos are analyzed with a camera-motion estimation algorithm (structure-from-motion) and labeled manually with a specific style. By considering spectral properties of location, orientation and acceleration, our solution learns camera motion details. Consequently, an arbitrary virtual base motion, defined in any conventional animation package, can be automatically modified according to a user-selected style. In an animation package the camera motion base path is typically defined by the user via function curves. Another possibility is to obtain the camera path by using a mixed reality camera in motion capturing studio. As shown in our experiments, the resulting shots are still fully artist-controlled, but appear richer and more physically plausible.
Keywords: style transfer, camera shake, camera motion estimation, structure-from-motion
Keywords: camera motion estimation, camera shake, structure-from-motion, style transfer
SWD: Kameraführung, Filmgestaltung, Postproduktion
The ability to change the camera viewpoint over time - camera motion - is a key ingredient of expressive film making. Different movies, TV productions, or cinematographers often adhere to specific styles of camera motion. Some famous directors even have a stylistic "trademark" on how they employ camera motion [ Bac96 ].
The style in which a camera is moved through the scene can substantially change the perception of the scene. Different camera motion styles are often used to highlight certain moods or situations and can be an important narrative element, e.g., fast-paced camera motion in action scenes. In some movies, e.g., Cloverfield or Blair Witch Project, a shaky camera style adds to the impression of the story being non-fictional and the scenes being recorded by the protagonists themselves with a consumer hand-held camera.
Figure 1. Example camera motion extracted from an example video (left), which is then transferred as details to a base virtual camera motion in a virtual scene (right).

In most real-world productions, however, strong camera shake is not desired and a multitude of different equipment is used to reduce the high frequencies in the camera motion paths. This is achieved by steadicam systems or by mounting the camera to a dolly, a boom, or a crane. But even well-stabilized camera systems still exhibit shake. Observers got used to these more or less subtle deviations, and tend to classify scenes without camera shake as unnatural.
Camera animations in virtual worlds are usually generated by an animator who designs a camera motion by assembling a motion path from multiple mathematically-defined smooth motion curves. These motion curves contain no camera shake at all. In a virtual scene the animator has more artistic freedom in designing the camera path and can test more options than a cinematographer at a real-world set. Nevertheless, the results are often not convincing and have an artificial appearance.
Creating a convincing camera movement manually is a challenging task. Therefore, in this paper we present an approach to transfer camera shake from real videos onto an artificially designed camera motion path in a virtual scene. These additional subtle or strong movements increase the feeling of unpolished, direct realism. The resulting virtual camera motions can still be designed by an artist, but exhibit a richer and more physically plausible look.
Our solution consists of three stages: the data acquisition stage, the analysis stage and the query stage. In the initial data acquisition stage, our system extracts camera motion from a video database using computer vision techniques. In the second stage, the analysis stage, we decompose this camera motion into a base and a detail component and store it, so that base motions can define a query for suitable detail motions. In the final query stage, a user provides base motions using common animation techniques, like three-dimensional spline editing, and the system adds suitable details interactively. A virtual path with plausible details can thereafter be used to drive a camera in a virtual scene. In addition to camera motion designed in an animation package, mixed reality cameras have become increasingly popular in movie productions. They allow the director to seamlessly interact with both the real and virtual part of the scene directly on set by using motion capturing technology. We show how our algorithm can be applied to the input generated by a mixed reality camera in the post-processing stage in order to achieve a variety of different effects at little to no additional cost during on-set production.
This paper is structured as follows. We review related work in Section 2. Section 3 gives details about our approach, and in Section 4 applications and results are presented. The results are discussed in Section 5 before concluding in Section 6.
In this paper, we combine ideas from camera control and animation processing, with a recent trend in rendering and image processing which seeks to extract visual style.
Our system relates to camera control for static [ Bli88, FvDFH95, GW92 ] or animated scenes [ KK88, DGZ92, HCS96 ], and overlaps with storytelling [ SD94 ] in a continuous range from complete artist camera control to complete computer control. Our approach is orthogonal to and could be combined with such approaches because we maintain the original artist-defined path and only enrich it by transferring camera motion styles. Recent work in camera control [ LC08, OSTG09 ] could also benefit from the stylization of the generated motion paths.
The formation of images using a certain camera is described by its internal parameters. Projective parameters can be determined using images of known scenes [ Tsa86 ] and image sequences allow to capture the radiometric response [ DM97 ]. Recently, image collections [ KAGN08 ] were used to calibrate brands of cameras. A separation of base and detail information of camera motion of real observations has not been described yet.
Camera shake can be an unwanted effect and can be removed using camera stabilization [ MC97 ]. Buehler et al. [ BBM01 ] extracted 3D camera motion using structure-from-motion to de-shake and then warp the images according to this new motion. Content preserving warps can be used to reliably warp the image into the stabilized 3D view [ LGJA09 ]. After extracting a 3D camera motion path, Gleicher and Feng [ GL07 ] project this path onto the closest "cinematographic" path to make a video appear more directed.
Moving a camera during its (virtual) film exposure also influences the scene capture and leads to motion blur [ JKZS10 ]. For camera shake, the movement is complex, leading to a complicated blur kernel and, hence, a distinct look (cf. Fig. 2)
Figure 2. Four frames from an animation with complex blur kernels generated by our system for a walking style motion.

Separating a signal into style (sometimes also called the "form", the "look" or the "decoration") and content (sometimes called "base" or "guide") is of interest in many classic media, such as traditional painting [ Liv02 ], or even dancing, where variations are added on top of a basic movement. Tackling this challenge computationally allows, among other applications, to perform style transfer, that is, to extract a style from a signal and apply it to different content.
Image analogies [ HJO01 ] learn the style of a certain image filter by analyzing several before-after examples, similar to approaches in texture synthesis. Adjustments of tonal values (histogram matching) [ RAGS01, BPD06 ] are often successful in reproducing a distinct photographic look.
Surfaces, like landscapes, also have distinct statistical properties that follow a guide signal [ FFC82 ]. For the special case of human face geometry Golovinskiy et al. [ GMP06 ] derived a statistical model to synthesize details. Style transfer has also been applied to animation, e. g. , of humans [ BW95, BH00, LHP05 ], to transfer motion between characters [ Gle98 ] or to cartoon characters [ WDAC06 ], and to motion editing [ WMZ06 ].
Texture synthesis can be seen as extracting only the decoration and then re-synthesizing it to fill a certain space [ HB95, EL99, WLKT09, OAIS09 ]. In [ MKC06 ], Mertens et al. synthesize texture details, but use the underlying geometry as a guiding signal.
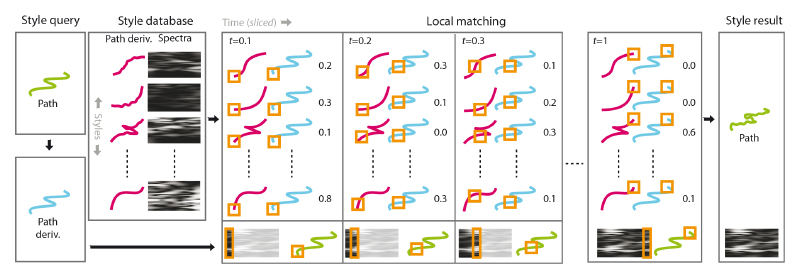
Our system for camera motion style transfer consists of three phases: the data-acquisition phase, the learning phase and the query phase. During the acquisition phase, a database of camera motions is built from a selection of input videos containing different types of camera motion. Thereby, the camera motion information is extracted from the videos by a fully-automatic camera motion estimation algorithm. In the learning phase, the camera motion paths are separated into low and high frequencies (base and detail layer). In the query phase an animator can specify a query camera motion path using a standard modeling tool, e.g., by key-framing or, in our case, by editing three-dimensional splines. The base layer of the query camera motion is compared to the base layers of the videos in the database. The detail layers of the locally-well-matching paths are used to add suitable details to the stylized camera path (cp. Fig. 3).
Figure 3. Stylization overview: Input to the stylization is a smooth virtual camera path (blue line): the style query. A style database of camera paths (red lines) and their time varying spectra (blocks) was build in a pre-process. To perform the query, the camera path (blue line) is locally matched against smooth versions of all training examples (pairs of red and blue paths) at every point in time (orange square) resulting in a distance (number). For each time slice, a new spectrum (orange block at bottom) is generated as a linear combination of the database spectra, weighted by the inverse distance. Note, that orange blocks are slices in time: When fixing time, time-varying spectra are just spectra. Finally, we produce the style result by adding noise with a matching time-varying spectrum.
For the data acquisition we used selected videos of varying camera motions from different sources, including casual home video, feature films, and TV series. All input videos had a sample rate of 25 Hz. We exclude all forms of virtual camera motions, such as computer animated footage.
From this data, we reconstruct the three-dimensional
camera-motion paths originally used in the shooting of the
footage. Our fully automatic camera motion estimation
approach [
TB06
] employs well-known computer vision
techniques [
PGV04, GCH02, HZ00
] to extract the
camera position, orientation, and focal length for each
frame of the video. As the absolute scale of the scene
cannot be determined from the videos, we convert
the automatically obtained result into an absolute
framework by manually specifying one spatial reference
unit for each video. The resulting camera motion is a
regularly-sampled time series of camera positions and
orientations. Such a representation has six degrees of
freedom per frame, where position is stored as an
Euclidean 3-vector x and orientation as a unit quaternion
q. We denote the i-th out of N camera motion paths
representing positions and orientations as a time-varying
mapping from time t to position
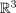 and orientation
and orientation
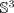 :
:
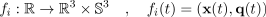 .
.
Further, we denote the matrix corresponding to a transformation (x,q) as T(x,q) and the inverse as T-1 . The resulting data is called the camera-motion database. The camera motion estimation approach also extracts the intrinsic camera parameters, such as the focal length. Since we assume the stylistic information to be largely dominated by the variation in the extrinsic camera parameters, we keep all intrinsic parameters unchanged during the stylization.
Border modes In practice, f is only available over a
limited time range [0,tmax]. If required, we replace the
variable t by a modified version
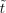 to mimic the extension
of the definition of f to
to mimic the extension
of the definition of f to
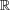 . We denote the replacement
scheme as border mode. Let u be defined as
. We denote the replacement
scheme as border mode. Let u be defined as
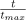 .
For the default border mode, repeat, t is replaced
by
.
For the default border mode, repeat, t is replaced
by
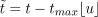 .
.
This causes f to be repeated periodically; as soon as the required t reaches the end of the motion path it wraps around and restarts at the beginning. The second border mode, ping-pong, is essentially a mirrored repeat:
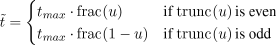 ,
,
with frac(·) being a function that selects the fractional part of a number and trunc(·) being a function that truncates a number to its integer part. Instead of immediately restarting at the beginning, the details of the motion path are traversed in reverse order before wrapping around again.
In the analysis phase, we use the camera-motion database to establish a relation between base camera motion fbase and camera-motion details denoted as fdetail , which we call the camera-style model. This model synthesizes the detail statistics of a certain base motion with respect to a chosen camera style at a certain point in time. Precisely, the base motion will act as the key and the details as the value of a style relation. We decompose the camera motion into base and detail as follows (cf. Fig. 4).
Figure 4. We decompose the original camera animation path into a smooth base path as well as details which are stored in the local frames of the base path.
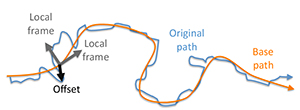
Base The base motion, is a smooth version of the
camera path, i. e., the basic curving of the camera path.
For smoothing, we use a Taubin filter [
Tau95
]
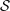 of
approximately 0.5 seconds support:
of
approximately 0.5 seconds support:
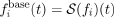 .
.
In other words, all motion finer than 0.5 seconds is considered a detail, all coarser motions are included in the base motion. Taubin's filter is a non-shrinking filter, which is important for the two boundary vertices at 0 and tmax . We use 100 iterations with simple (1,2,1) weights.
Detail Next, we define the detail camera motion as the original input camera pose, but in the reference frame of the base path (an offset transformation)
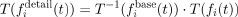 .
.
E. g., a camera motion that is already smooth will not lead to any details at all, whereas areas with a strong deviation between the smooth and the non-smooth version of the path have more details - as expected. Note, that the non-shrinking property of the Taubin filter [ Tau95 ] prevents spurious detail values at the boundaries. Further, shrinkage would influence the extraction and shift base content in the detail layer.
Finally, we perform local frequency analysis (Gabor decomposition) of this offset transformation leading to a time-varying spectrum:
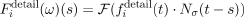
A Gabor transform is a Fourier transform
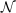 with a
time-varying parameter s. This parameter is used to mask
the input signal's intensity with a Gaussian and give more
weight to the part of the signal that is close to s in
time.
with a
time-varying parameter s. This parameter is used to mask
the input signal's intensity with a Gaussian and give more
weight to the part of the signal that is close to s in
time.
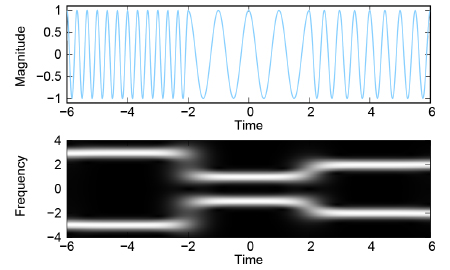
Fig. 5 shows a Gabor decomposition for a very simple input signal. For Gabor filtering, we use a σ of around 0.2 units, that is, at every point in time we locally consider the frequencies of 0.1 units to the left and 0.1 units to the right in time.
Figure 6. Example spectra extracted from two camera motion paths using a Gabor transform. The top row shows the spectra of a path obtained from a sequence filmed while making a right turn with a bicycle; the bottom row depicts the spectra of a path reconstructed from a running sequence in the movie Cloverfield. From left to right: orientation, x-, y-, and z-component; position, x-, y-, and z-component.
Query key To compare query keys, we use the Euclidean differences of the second derivative of the base:
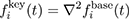 .
.
We compute the derivative ∇2 using simple forward differentiation, which works well as fi key(t) is already smooth. We use the derivative because it correlates best with the detail movements. For example, moving faster (large derivative) gives stronger details, as well as moving around a corner (derivative with multiple non-zero components) results in more shake than a straight movement (only a single non-zero component).
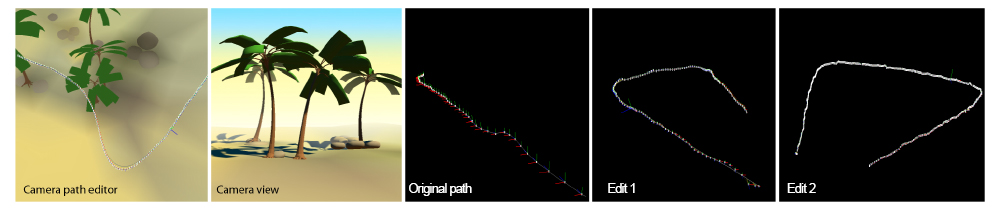
In the query phase, a user provides a base camera movement gbase(t). Its second derivative gkey(t) is matched against all elements fj key in the database that correspond to the desired style. Each database element has an associated spectrum Fi detail(ω)(s) that encodes the detail statistics. These statics are linearly weighted separately for each time slice to yield the detail statistics Gdetail(ω)(s) that are synthesized by:
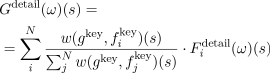 ,
,
with the time-varying weighing w
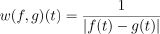 ,
,
where | | is a modified L2 norm that weights orientation and position with differing coefficients. (In practice, our scene scale allows us to use the same factor for both.) When computing w, the border mode extends both f and g to be defined for every t, allowing for sequences of different length.
We then re-generate motion details according to the
derived statistics Gdetail(ω)(s). For this, we rely on
uniformly distributed random numbers. These numbers
are interpolated on varying scales and are used to sample
according to the time-varying spectrum [
Per85, LLC10
].
We call
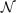 the operator that generates the signal according
to the given spectrum:
the operator that generates the signal according
to the given spectrum:
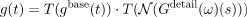 .
.
Note that the details - by design - will only share the spectrum of what was observed and are not actual copies. This means that the details are non-repetitive, even if they are synthesized for a very long motion path (cf. Fig. 9).
This Section discusses two cases of application of our system and provides the results of the corresponding experiments. In the first case (Section 4.1), the user provides an input camera path defined by a spline curve. In the second case (Section 4.2), the input path is the motion path of an on-set mixed reality camera.
To conduct our experiments, we first generated a camera motion database with a total of 48 automatically analyzed sequences. These sequences are manually labeled with styles. We used 5 different labels: walking (17 sequences), running (2 sequences), bicycle (16 sequences), skateboard (9 sequences), and helicopter (4 sequences). Fig. 6 shows two example spectra extracted from a biking and a running sequence.
While motion is difficult to reproduce on paper, depicting animation details is hardly possible. We therefore refer to the accompanying video for a visualization.
Our system lets a user load a virtual scene that can be inspected in 3D in real-time. The user can define a camera motion path by placing splines in the scene. The system then synthesizes detail for that motion path interactively by querying the current path in the database of details.
Furthermore, we can hallucinate and synthesized motion frequencies that were not even present in the original 25 Hz motion observation. We do this by fitting a line in the spectral domain into the spectrum and extrapolate frequencies above the original data's cut-off frequency. When using a high-refresh-rate display (e. g. , 120 Hz), these supplementary details add further subtle movements that increase realism.
In a first example (please see the supplemental video), a user has set up a virtual scene (which is also shown in the teaser figure) and selects different style tags that alter the camera motion style. First, the user selects a simple walking motion from a certain movie as style. Our system transfers this walking style to a different camera animation. The result is a motion that includes a curved path instead of the straight motion that was present in the original input movie. Furthermore, the motion is several times longer than the original input style example.
The user then selects running-style motion details for a faster motion. Note that the speed changes the details. Then, the user selects a bicycle style, where mainly details in the y component of the position, as well as high-frequency rotational noise is present. Finally, when selecting the skateboard style, only high frequency positional noise remains.
Figure 7. An edit session using our system. From left to right: Users manipulate a spline in a 3D world using an existing framework including an interactive camera preview. Our system adds the details from the style example to two edited path shapes. Note, how the edited path shapes are different from the style example (which is a straight line) in shape and duration, but the details are similar. An animated version of this figure can be found in the supplemental video.
In a second example (cf. Fig. 7 ), the user modifies a camera path, and details are synthesized interactively while the path changes. The details adapt to the shape of the path, i. e. , details orthogonal to the path remain orthogonal, even if the path is deformed. Finally, the users selects the strength and cutoff frequency of the details to reach the desired result.
Having captured the camera-shake spectrum, we
made certain findings. We can confirm, that - similar
to many things in nature - the power spectrum of
camera shake is indeed
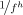 , with an h ≈ 2, which is the
same as, e. g. , for the intensity distribution in natural
images.
, with an h ≈ 2, which is the
same as, e. g. , for the intensity distribution in natural
images.
Modern movie and video game productions have seen an increase in the use of mixed reality cameras [ OT99 ].
Traditional cameras can only provide feedback about objects which are physically present at the set. In contrast to this, a mixed reality camera is a physical device used to obtain a preliminary rendering of a virtual scene. The device's physical position is captured and stored by the on-set motion capturing equipment, providing the director with immediate real-time feedback. In addition, the motion data is later used to drive the camera positions used for rendering in post-processing. A mixed reality camera therefore provides viable input data for our algorithm.
To illustrate how our system can be applied to camera paths originating from such a system, we retrofitted a handheld consumer camera with a makeshift LED assembly and captured several camera motion paths in a motion capturing studio (cf. Fig. 8). Once the camera path has been recorded, the processing pipeline remains largely unchanged. The reconstructed motion path, or a smoothed version of it, is substituted for the artist-created camera motion path as query key gkey(t) in the query phase. We are thereby able to recreate a wide variety of different motion models, while only minimal precautionary measures have to be taken in advance.
Figure 8. Mixed reality camera: Capturing of input camera sequence by state-of-the-art motion capturing equipment (top left), data processing and camera path extraction (top right), smoothed input camera path (bottom left), camera path after a different motion style has been transferred (bottom right).

There are alternatives to our detail extraction approach. One option is to subtract a smoothed version of the path from the original path and directly rely on the difference. We did not use this approach, because the resulting animations are always repetitive and contain copied details (cp. Fig. 9).
Figure 9. Synthesizing details from a time-varying spectrum instead of adding them directly avoids repetition. From left to right: Given a base path and a preview, adding details in Euclidean space can lead to repeating details (arrows), whereas Gabor details do not repeat and only share their spectral properties with the style example.

The quality of the Gabor time-frequency resolution is limited, because we have to detail with a relatively limited sampling rate, compare to, e. g. , sound samples (25 Hz camera animation vs. typical 44 kHz audio).
Depending on the motion, our choice of 100 iterations for the Taubin filter might not be optimal. In practice, picking a higher smoothing will shift base information into the details, while doing less smoothing will only cause small parts of the signal to be detected as details. The details are finer for some paths, while they are coarser for others, and so choosing this parameter globally is a compromise. Nevertheless, due to our fixed input sampling rate, we found that our indicated global values make sense and behave well in most cases. In general, it would be interesting to find criteria that separate base and detail on a perceptual basis and for varying frame rates. Fig. 10 shows extracted details for different cut-off frequencies.
Figure 10. Details of different cut-off frequencies (in number of Taubin iterations). For very high values (200 and more for a 100 sample input style example), the complete style example is considered a detail and a straight line starts to look like the style example itself.
The system relies on the filtering to remove all unwanted motion path components from the extracted details. The context of the scene is effectively ignored; this includes the interaction of the camera with dynamic objects in the scene. If the filter settings cannot be chosen in a way that eliminates the (probably unwanted) interactions but still retains the desired details, additional steps have to be taken. The motion paths can be split into appropriate sub-paths, which are then annotated correctly with the interaction type. This prevents the system from using outlier motion segments for the synthesis. Detailed and concise annotations provided, even the excluded segments could then be used at corresponding locations. In settings where accurate path planning is crucial due to constraints of the virtual environment, e. g. , confined spaces that provide very limited freedom of movement to the camera, the added details may have to be controlled to avoid the introduction of artifacts. This can be achieved by applying a logarithmic damping to the details once their magnitude exceeds a given threshold.
We presented a system to add plausible camera motion details to a virtual camera motion. The system synthesizes details at interactive rates, so novel camera animations can be readily inspected in real-time. We avoid repetitive structures in the motion and are able to mimic various styles. The system can also be applied to mixed reality cameras in order to achieve a large variety of effects in post-processing without requiring precautionary measures during the on-set part of the production.
In future work, we would like to find physical camera parameters (i. e. , weight, mass tensors), by applying inverse physical modeling to the extracted camera motion data. Once such data is available, novel camera paths could also take a physical model into account. We would also like to further improve the efficiency of the database queries. Currently, the query time is governed by the number and length of motion paths in the database, since all entries annotated with the desired style have to be evaluated to decide which one of them fits the query data best. If we were able to hash the keys in an appropriate fashion, constant-time lookup could make this method feasible for the on-line generation of motion path details. This could be useful for camera motion planning in video game and navigation applications, where the available budget of computation time puts tight constraints on the database search.
Further, structuring the detail space according to spectral properties could be used to derive priors for other applications, i. e. , automatic classification of footage. In the context of rendering, realistic motion blur [ JKZS10 ] is achieved by convolving with the full point spread function (PSF) of the camera movement during exposure (cp. Fig. 2 ). We could use our spectrum extrapolation to generate intra-frame details from tracking data available only at frame resolution. The resulting motion blur would agree better with the expected spectrum of the camera movement. Finally, our results might also be of interest for stabilization, which could be easier, if the expected spectrum of camera shake can be modeled.
This work has been partially funded by the Max Planck Center for Visual Computing and Communication (BMBF-FKZ01IM10001) and the Intel Visual Computing Institute.
[Bac96] Max Ophüls in the Hollywood Studios 1996 Rutgers University Press New Brunswick, NJ 0813522919
[BBM01] Non-Metric Image-Based Rendering for Video Stabilization Proc. CVPR, 2001 pp. 609—614 0-7695-1272-0
[BH00] Style machines Proc. SIGGRAPH, 2000 ACM New York, NY, USA pp. 183—192 1-58113-208-5
[Bli88] Where am I? What am I looking at? IEEE Comput. Graph. Appl., 1988 4 76—81 0272-1716
[BPD06] Two-scale tone management for photographic look ACM Trans. Graph. (Proc. SIGGRAPH), 2006 3 637—645 0730-0301
[BW95] Motion signal processing Proc. SIGGRAPH, 1995 ACM New York, NY, USA pp. 97—104 0-89791-701-4
[DGZ92] CINEMA: A system for procedural camera movements Proc. Symposium on Interactive 3D Graphics, 1992 ACM New York, NY, USA pp. 67—70 0-89791-467-8
[DM97] Recovering high dynamic range radiance maps from photographs Proc. SIGGRAPH, 1997 pp. 369—378 New York, NY, USA article no. 31 0-89791-896-7
[EL99] Texture Synthesis by Non-Parametric Sampling 1999 IEEE Computer Society Washington, DC, USA pp. 1033—1038 0-7695-0164-8
[FFC82] Computer rendering of stochastic models Commun. ACM, 1982 6 371—384 0001-0782
[FvDFH95] Computer Graphics: Principles and Practice in C Addison-Wesley Professional 1995 2nd edition 0-201-84840-6
[GCH02] Accurate Camera Calibration for Off-line, Video-Based Augmented Reality Proc. IEEE and ACM International Symposium on Mixed and Augmented Reality, Darmstadt, Germany 2002 p. 37 0-7695-1781-1
[GL07] Re-cinematography: improving the camera dynamics of casual video Proc. MULTIMEDIA, 2007 pp. 27—36 978-1-59593-702-5
[Gle98] Retargetting motion to new characters Proc. SIGGRAPH, 1998 ACM New York, NY, USA pp. 33—42 0-89791-999-8
[GMP06] A statistical model for synthesis of detailed facial geometry ACM Trans. Graph. (Proc. SIGGRAPH), 2006 3 1025—1034 0730-0301
[GW92] Through-the-lens camera control SIGGRAPH Comput. Graph., 1992 2 331—340 0097-8930
[HB95] Pyramid-based texture analysis/synthesis Proc. SIGGRAPH, 1995 ACM New York, NY, USA 229—238 0-89791-701-4
[HCS96] The virtual cinematographer: a paradigm for automatic real-time camera control and directing Proc. SIGGRAPH, ACM New York, NY, USA 1996 pp. 217—224 0-89791-746-4
[HJO01] Image analogies Proc. SIGGRAPH, 2001 ACM New York, NY, USA pp. 327—340 1-58113-374-X
[HZ00] Multiple View Geometry in Computer Vision 2000 Cambridge University Press 0-521-62304-9
[JKZS10] Image deblurring using inertial measurement sensors ACM Trans. Graph. (Proc. SIGGRAPH), 2010 4 1—9 article no. 30 0730-0301
[KAGN08] Priors for Large Photo Collections and What They Reveal about Cameras Proc. ECCV, 2008 Springer-Verlag Berlin, Heidelberg Lecture Notes in Computer Science pp. 74—87 978-3-540-88693-8
[KK88] A simple method for computing general position in displaying three-dimensional objects Comput. Vision Graph. Image Process., 1988 1 43—56 0734-189X
[LC08] Andreas Butz Brian Fisher Antonio Krüger Patrick Olivier Marc Christie (Eds.) Real-Time Camera Planning for Navigation in Virtual Environments Proceedings of the 9th International Symnposium on Smart Graphics, Springer Lecture Notes in Computer Science pp. 118—129 2008 978-3-540-85410-4
[LGJA09] Content-preserving warps for 3D video stabilization ACM Trans. Graph. (Proc. SIGGRAPH), 2009 3 1—9 article no. 44 0730-0301
[LHP05] Learning physics-based motion style with nonlinear inverse optimization ACM Trans. Graph. (Proc. SIGGRAPH), 2005 3 1071—1081 0730-0301
[Liv02] Vision and Art: The Biology of Seeing Harry N. Abrams 2002 0-8109-0406-3
[LLC10] State of the Art in Procedural Noise Functions Eurographics 2010, State of the Art Reports (STARs), 2010 Helwig Hauser Erik Reinhard (Eds.) Eurographics Association Eurographics
[MC97] Evaluation of Image Stabilization Algorithms DARPA Image Understanding Workshop (DARPA97), 1997 pp. 295—302
[MKC06] Texture Transfer Using Geometry Correlation Proc. Eurographics Workshop on Rendering, 2006 pp. 273—284 3-905673-35-5
[OAIS09] Animating Pictures of Fluid using Video Examples Comput. Graph. Forum, 2009 2 677—686 1467-8659
[OSTG09] Visibility Transition Planning for Dynamic Camera Control Proceedings of the 2009 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, SCA '09, 2009 ACM New York, NY, USA pp. 55—65 978-1-60558-610-6
[OT99] Mixed reality: Merging real and virtual worlds 1999 Springer-Verlag New York 3540656235
[Per85] An image synthesizer Proc. SIGGRAPH, 1985 ACM New York, NY, USA pp. 287—296 0-89791-166-0
[PGV04] Visual Modeling with a Hand-Held Camera Int. J. Comput. Vision, 2004 3 207—232 0920-5691
[RAGS01] Color Transfer between Images IEEE Comput. Graph. Appl., 2001 5 34—41 0272-1716
[SD94] IDIC: Assembling video sequences from story plans and content annotations Proc. Intl. Conf. on Multimedia Computing and Systems, 1994 pp. 30—36 0-8186-5530-5
[Tau95] A signal processing approach to fair surface design Proc. SIGGRAPH, 1995 ACM New York, NY, USA pp. 351—358 0-89791-701-4
[TB06] Voodoo Camera Tracker Digilab, 2006 Free download at http://www.digilab.uni-hannover.de.
[Tsa86] An Efficient and Accurate Camera Calibration Technique for 3-D Machine Vision Proc. CVPR, 1986 pp. 364—374
[WDAC06] The cartoon animation filter ACM Trans. Graph. (Proc. SIGGRAPH), 2006 3 1169—1173 0730-0301
[WLKT09] State of the Art in Example-based Texture Synthesis Eurographics 2009, State of the Art Reports (STARs), 2009 Eurographics Association pp. 93—117.
[WMZ06] On-Line Motion Style Transfer ICEC Lecture Notes in Computer Science Springer Berlin, Heidelberg pp. 268—279 2006 978-3-540-45259-1
Volltext ¶
-
 Volltext als PDF
(
Größe:
11.4 MB
)
Volltext als PDF
(
Größe:
11.4 MB
)
Lizenz ¶
Jedermann darf dieses Werk unter den Bedingungen der Digital Peer Publishing Lizenz elektronisch übermitteln und zum Download bereitstellen. Der Lizenztext ist im Internet unter der Adresse http://www.dipp.nrw.de/lizenzen/dppl/dppl/DPPL_v2_de_06-2004.html abrufbar.
Empfohlene Zitierweise ¶
Christian Kurz, Tobias Ritschel, Elmar Eisemann, Thorsten Thormählen, and Hans-Peter Seidel, Generating Realistic Camera Shake for Virtual Scenes. JVRB - Journal of Virtual Reality and Broadcasting, 10(2013), no. 7. (urn:nbn:de:0009-6-38335)
Bitte geben Sie beim Zitieren dieses Artikels die exakte URL und das Datum Ihres letzten Besuchs bei dieser Online-Adresse an.


